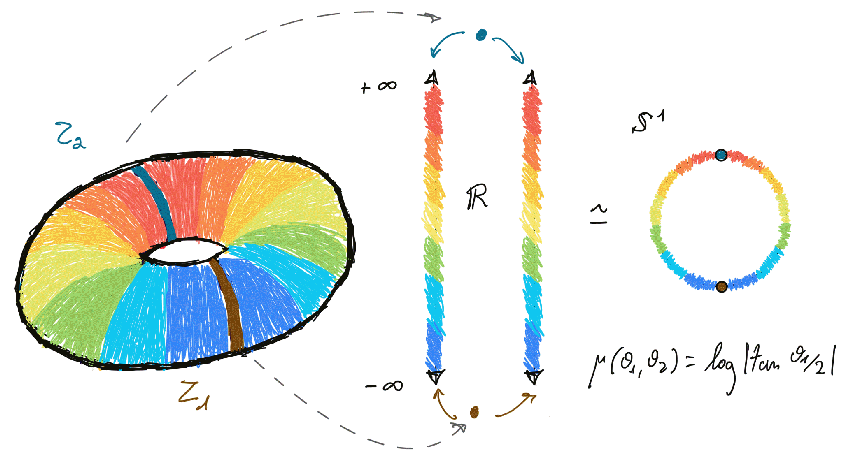Geometry and Dynamics of Singular
Symplectic manifolds
Henan University by Eva Miranda
Public
Lecture takes place on October 11 at 13h CET, 19h Kaifeng time
Connecting data for Public
Lecture:
Zoom Id: 5673065241
password: 123456
Undecidability of certain
fluid paths, the Navier-Stokes problem and 29000 rubber ducks lost in the ocean

This course is part of the
Overseas Distinguished Lectureship Program at the University of Henan in Kaifeng
NEW CONNECTION DATA!
-
The new Zoom link for lecture 2 and
on:
New Zoom ID: 815 7127 3363
Code: 123456

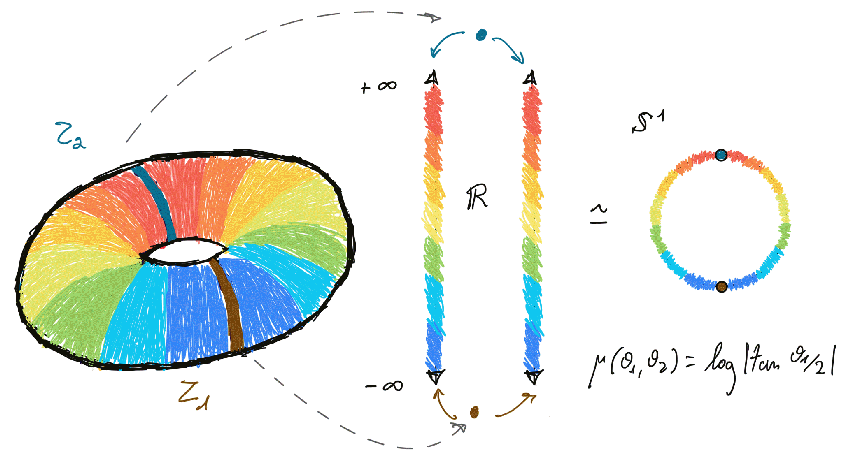
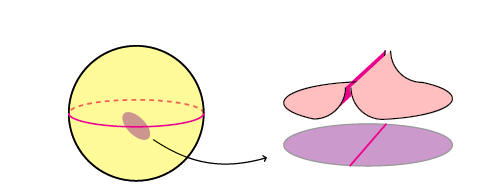
Figure on the top: Image
of the moment map of a b-torus (courtesy of Pablo Nicolás, a student of the
course). Observe that this b-moment map is circle valued. Figure on the bottom
representation of a b-map on a b-sphere.
Summary: b-Calculus was introduced by Richard Melrose when
considering pseudodifferential operators on manifolds with boundary. Later on,
Ryszard Nest and Boris Tsygan applied these ideas to study the deformation
quantization of symplectic manifolds with boundary.
The purpose of this minicourse is to unravel the geometrical structures (b-symplectic
structures) behind this picture and describe some applications to Dynamical
systems. b-Symplectic manifolds are Poisson manifolds which are symplectic away
from an hypersurface and satisfy some transversality condition. b-Symplectic
manifolds lie "close enough" to the symplectic category and indeed their study
can be addressed using an "extended" De Rham complex. In particular many
peculiarities from Symplectic manifolds are shared with b-symplectic manifolds.
Using these ideas, we will study normal form theorems, action-angle theorems,
toric actions and applications to KAM theory. At the end of the minicourse we
present other singular symplectic structures such as folded symplectic
structures and b^m-symplectic structures (for which the transversality condition
is relaxed) and explain how they are related to b-symplectic and symplectic
structures.
We will give a general overview of the theory using some examples in celestial
mechanics as leitmotiv. For some of them (like double collision), we can even
construct b^m-symplectic structures and m-folded structures. This apparent "duality"
will be used as an excuse to closely explore the relation between the $b^m$-symplectic
category with the symplectic and folded symplectic category. This relation
depends surprisingly on the parity of m and is given by a desingularization procedure called deblogging. Time permitting, several applications of deblogging
to dynamics and quantization will be presented.
Syllabus/Scheme of the
lectures
The planning of the lectures would be the following one:
Title: Geometry and Dynamics of Singular Symplectic Manifolds
Summary: We will describe a novel geometrical approach to classical problems
in Celestial Mechanics concerning collisions. The upshot of our methods is
that the singularities (collisions, infinity line) are included in the
geometrical techniques(as b-symplectic manifolds, b-contact manifolds). We
will focus on the geometry and Dynamics of these manifolds and describe
several techniques such as desingularization, normal forms, action-angle
coordinates and perturbation theory used in this study.
Planning with description of contents per day.
September 7 Overture: Introduction to the course. Basic definitions
in Symplectic Geometry and motivation for b-symplectic geometry. B-symplectic
manifolds as Poisson manifolds.
September 9 Melrose language of b-forms. b-symplectic forms on
b-Poisson manifolds. The geometry of the critical set. More degenerate forms
b^m-symplectic forms and b^m contact forms. Desingularization of b^m-forms.
September 14 The path method for b^m-symplectic structures. Local
normal form (b^m-Darboux theorem) and extension theorems. b^m-Structures to
the test: Examples in Fluid Dynamics and Celestial Mechanics. The b-symplectic
and b-contact geometry of the restricted three body problem and of Beltrami
fields. Application: Finding periodic orbits for trajectories of a satellite
in the restricted three body problem.
September 16 Exercise session
September 21 (POSTPONED DUE TO NATIONAL FESTIVITY IN CHINA)
September 23 More symmetries: Toric actions, action-angle
coordinates and Integrable systems on b^m-symplectic manifolds. Applications:
Perturbations of integrable systems and KAM theory.
September 28: Exercise session
September 30: Some classical problems for b^m-symplectic and b^m-contact
manifolds. Examples in Celestial Mechanics. Periodic Orbits. The (singular) Weinstein conjecture.
October 5: Finale:
A magic mirror between singular contact geometry and singular Fluid Dynamics.
Applying Uhlenbeck's results to find escape orbits in Celestial Mechanics. Open problems.
Material:
(passcode: KO8i^i77)
Videos of the course :
Bibliography:
- [BDMOP]
R. Braddell, A. Delshams, E. Miranda, C. Oms and A. Planas,
An invitation to Singular Symplectic Geometry ,
arXiv:1705.03846, accepted at International Journal of Geometric Methods in
Modern Physics, 2017.
- [CGP] A. Cannas, V. Guillemin, A.R. Pires, Symplectic Origami , International
Mathematics Research Notices, no.18, pp 4252-4293, 2011.
- [CM] R. Cardona and E. Miranda, Integrable systems on singular
symplectic manifolds: from local to global, IMRN to appear, 2021,
https://arxiv.org/abs/2007.10314
- [DKM] A. Delshams, A. Kiesenhofer, E. Miranda, Examples of integrable
and non-integrable systems on singular symplectic manifolds,
J. Geom. Phys.
115 (2017), 89–97.
- [DZ]
Dufour, Jean-Paul;
Zung, Nguyen Tien Poisson structures and their
normal forms.
Progress in Mathematics, 242. Birkhäuser Verlag, Basel, 2005.
xvi+321 pp. ISBN: 978-3-7643-7334-4; 3-7643-7334-2
- [DKRS] A. Delshams, V. Kaloshin, A de la Rosa, T. M.-Seara, Global
instability in the elliptic restricted three body problem, arXiv:1501.01214.
- [Du] J.J. Duistermaat, On global action-angle coordinates. Comm. Pure
Appl. Math. 33 (1980), no. 6, 687-706.
- [GMP1] V. Guillemin, E. Miranda, and A. Pires, Codimension one
symplectic foliations and regular Poisson structures. Bull. Braz. Math. Soc.
(N.S.), 42(4):607-623, 2011.
- [GMP2] V. Guillemin, E. Miranda, and A. Pires,
Symplectic and Poisson geometry on
b-manifolds. Adv. Math. 264 (2014), 864-896.
- [GMPS1] V. Guillemin, E. Miranda, A. R. Pires and G. Scott,
Toric actions on b-symplectic
manifolds, Int Math Res Notices Int Math Res Notices (2015) 2015 (14):
5818-5848.
- [GMPS2] V. Guillemin, E. Miranda, A. Pires, and G. Scott.
Convexity for Hamiltonian torus
actions on b-symplectic manifolds,
Math. Res. Lett.
24 (2017), no. 2, 363–377.
- [GMW1] V. Guillemin, E. Miranda, J. Weitsman,
Desingularizing b^m-symplectic
structures,
- [GMW2] V. Guillemin, E. Miranda, J. Weitsman, On geometric quantization
of b-symplectic manifolds, Adv in Math 2018.
- [LMV] C. Laurent-Gengoux, E. Miranda and P. Vanhaecke,
Action-angle coordinates for integrable systems on
Poisson manifolds.
Int. Math. Res. Not. IMRN
2011, no. 8, 1839–1869.
- [LPV]
Laurent-Gengoux, Camille;
Pichereau, Anne;
Vanhaecke, Pol Poisson structures.
Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of
Mathematical Sciences], 347. Springer, Heidelberg, 2013. xxiv+461
pp. ISBN: 978-3-642-31089-8.
- [MG]R. McGehee, Singularities in classical celestial mechanics.
Proceedings of the International Congress of Mathematicians (Helsinki,
1978), pp. 827-834, Acad. Sci. Fennica, Helsinki, 1980.
- [MO1] E. Miranda and C. Oms,
The Singular Weinstein conjecture, Advances in Math, 2021, Golden Open
access
- [MO2] E. Miranda and C. Oms, The geometry and topology of contact
structures with singularities,
https://arxiv.org/abs/1806.05638
- [MP] E. Miranda and A. Planas, Action-angle coordinates and KAM for
singular symplectic manifolds, monograph 100 pages, 2021.
- [W] A. Weinstein, The local structure of Poisson manifolds., J.
Differential Geom. 18 (1983), no. 3, 523-557.