Una firma digital estándar proporciona a una comunicación digital las propiedades de autenticación universal, integridad y no repudio. La primera propiedad quiere decir que todo el mundo puede verificar quién ha sido el usuario que ha calculado la firma digital y por tanto cuál es el origen de la comunicación digital. La segunda propiedad asegura que el mensaje recibido es exactamente igual al mensaje enviado, es decir que no ha sido alterado durante el envío. La última propiedad se refiere al hecho que el emisor de una comunicación firmada no puede negar posteriormente ser el autor de dicha comunicación.
Estas propiedades son básicas para asegurar unas comunicaciones digitales fiables; por tanto las firmas digitales son consideradas como el segundo pilar fundamental de la criptografía, junto con los sistemas de cifrado, y han recibido una atención similar por parte de la comunidad criptográfica. Eso quiere decir que los diferentes estándares criptográficos (ver por ejemplo los enlaces en la Sección 2) también recomiendan sistemas de firma digital y tamaños de claves concretos, tanto en el escenario de criptografía simétrica como en el escenario de criptografía asimétrica.
En lo que sí supera la firma digital al cifrado es en el número de extensiones y propiedades adicionales que se han propuesto al concepto básico original. Una lista de extensiones del concepto de firma digital existentes en la literatura incluiría, entre otras, las firmas ciegas, las firmas innegables, las firmas camaleónicas, las firmas nominativas, las firmas por delegación, las firmas agregadas, las firmas con confirmador, las firmas con verificador designado, las firmas de grupo, las firmas de anillo, las firmas transitivas, las firmas sanitizables, las firmas de umbral, las multi-firmas...
Repasar todas estas extensiones llevaría a un documento demasiado largo, así que hemos escogido seleccionar algunas de ellas, usando como criterio el número de aplicaciones a situaciones actuales de la vida real que pueden tener los sistemas de firma resultantes.
En un sistema de firma ciega participan dos usuarios, el firmante y el cliente. El firmante tiene su par de claves pública y privada, (pk, sk), como en un sistema normal de firma digital en un escenario de criptografía asimétrica. El objetivo del cliente es obtener una firma válida del firmante a un mensaje m, sin que el firmante obtenga ninguna información sobre el mensaje m. Se trata de un protocolo interactivo en el que cliente y firmante intercambian mensajes, que van calculando en función de los mensajes anteriores y en función de los valores que sólo cada usuario conoce (sólo el cliente conoce el mensaje m y sólo el firmante conoce la clave secreta sk). El resultado de la interacción es que el cliente puede calcular una firma σ tal que Vfy(pk,σ,m) → 1 (firma válida del mensaje m proveniente del firmante con clave pública pk).
Un sistema de firma ciega tiene que satisfacer dos propiedades de seguridad. Por un lado, un firmante no puede obtener ninguna información sobre los mensajes que está firmando (privacidad del mensaje). Por otro lado, un cliente que interactúa con un firmante, con éxito, un número ℓ de veces no puede ser capaz de obtener ℓ + 1 firmas válidas diferentes para la clave pública pk (infalsificabilidad).
El concepto de firma ciega fue propuesto por Chaum [17] y las dos aplicaciones que mencionaba en su artículo eran el voto electrónico (eVoting) y el dinero electrónico (eCash).
En voto electrónico, imaginemos que la junta electoral que gestiona el censo de votantes autorizados en una votación juega el papel de firmante en el sistema de firma ciega. Cada votante autorizado a votar será un cliente: acudirá a la junta electoral, le demostrará que está autorizado a participar en la votación (mostrando un DNI, por ejemplo) y juntos ejecutarán el protocolo de firma ciega, de manera que el mensaje privado del votante, m, sea su voto. El resultado del sistema será una firma válida de ese voto por parte de la junta electoral. Esa pareja de voto y firma puede ser depositada de manera anónima en la urna electoral: la validez de la firma será verificada por la entidad que realice el recuento, y los votos con firma válida serán los que se cuenten el el recuento final.
En dinero electrónico, podemos suponer que cada moneda electrónica tiene el mismo valor (por ejemplo, 10 euros). Cuando un cliente quiere obtener una moneda electrónica, acude al banco (que será el firmante) y le pide una moneda electrónica: el banco le quita 10 euros de su cuenta, y entonces ejecutan el protocolo de firma ciega, donde el mensaje privado del cliente es un número aleatorio m. Como resultado, el cliente obtiene una firma válida σ de m por parte del banco, que proporciona al comercio en el que quiera gastar 10 euros a cambio de algún producto. El comercio puede verificar que la firma es válida y cerrar la transacción. Después, el comercio acudirá al banco con la pareja (m,σ). El banco compara m con el resto de códigos de monedas que almacena en su base de datos de monedas gastadas; si no está allí y la firma es válida, el banco da 10 euros al comercio y añade el valor m a la lista de códigos de monedas ya gastadas.
Existen esquemas de firma ciega cuya seguridad se basa en problemas clásicos como RSA [7, 17] o el logaritmo discreto [46]. También se han propuesto esquemas de firma ciega (más eficientes) que utilizan entornos matemáticos más avanzados, por ejemplo los emparejamientos bilineales [8, 26].
Por último, también existen propuestas de sistemas de firma ciega con seguridad post-cuántica, basados en retículos euclideanos [51].
Las propiedades de autenticación y no repudio que otorga una firma digital básica a una comunicación digital a veces pueden ser no deseadas en algunas aplicaciones. Por ejemplo, a lo mejor una firma quiere demostrar que su autor es un usuario dentro de un determinado grupo de personas, pero sin especificar qué usuario concreto del grupo es el autor de la firma. De esa manera, una firma proporciona nivel de autenticación a nivel de grupo, pero proporciona al firmante anonimato dentro del grupo.
Esta idea se ha materializado de dos maneras diferentes en la literatura criptográfica, dando pie a las firmas de grupo y a las firmas de anillo. Las diferencias son las siguientes:
- En un sistema de firma de grupo, existe una autoridad de grupo que gestiona las entradas y salidas de miembros en el grupo; cuando un usuario entra en el grupo, recibe de la autoridad una información secreta de pertenencia al grupo, que luego podrá ser usada para calcular la firma en nombre de todo el grupo. El grupo dispone de una clave pública de grupo, que es la que puede usar cualquiera para verificar la validez de una firma de grupo.
- En un sistema de firma de anillo, no hay ninguna autoridad central. Cada usuario tiene su par de claves (pk, sk), y los grupos se van creando ad-hoc en el momento de firmar: un usuario junta su clave pública con otras claves públicas de otros usuarios para formar una lista (o un anillo) de usuarios que será el grupo origen de esa firma. Para verificar la validez de la firma, será necesario usar todas las claves públicas del grupo.
La existencia de una entidad central de confianza en las firmas de grupo hace que sea más fácil diseñar sistemas eficientes, por ejemplo produciendo firmas de grupo de tamaño constante (independiente del tamaño del grupo). En cambio, la mayoría de sistemas de firma de anillo propuestos en la literatura producen firmas cuyo tamaño depende del número de usuarios en el grupo.
Estos sistemas de firma anónima tienen que satisfacer, al menos, dos propiedades de seguridad. Por un lado el anonimato, que quiere decir que nadie (tal vez a excepción de la autoridad de grupo, en las firmas de grupo) puede distinguir qué miembro de un grupo es el autor real de una firma. Por otro lado, la infalsificabilidad, que quiere decir que un usuario (un atacante) que esté fuera de un grupo de usuarios no debe ser capaz de producir una firma válida en nombre de ese grupo de usuarios.
Las firmas de grupo y de anillo, unidas a las firmas basadas en atributos que explicaremos más adelante, son la herramienta principal para aplicaciones en las que se requieren a la vez un cierto nivel de autenticación (tener unas determinadas credenciales de pertenencia) y un nivel de anonimato. Algunos ejemplos de estas situaciones en la vida real pueden ser:
- Filtrar noticias a la prensa de manera fiable: tal vez un miembro de un gobierno o de un partido político quiere filtrar a la prensa una noticia pero de manera anónima, sin que nadie pueda acusarle de ser el origen de la filtración. Para ello, puede usar una firma de grupo o de anillo en el que el conjunto de posibles firmantes sea por ejemplo el conjunto de miembros del gobierno. De esa manera, la prensa dará credibilidad a la noticia.
- Acceso privado a recursos: para acceder a un determinado recurso físico o digital (puede ser la puerta de un gimnasio o una biblioteca, o bien partes protegidas de una página web), se puede implementar un sistema de control de acceso con privacidad, de manera que cuando un usuario quiera acceder a ese recurso, el sistema escoge un mensaje (un reto) aleatorio m. El usuario debe ser capaz de calcular una firma de grupo válida para ese reto m, tomando como grupo el conjunto de usuarios autorizados a acceder a ese recurso. Si la firma generada es verificada como válida por el sistema de acceso, el usuario puede acceder al recurso. El sistema mantiene el anonimato del usuario: sólo se filtra el hecho de que es un usuario autorizado (o no) a acceder a ese recurso.
Existen propuestas de sistemas de firma de grupo y de firma de anillo en todos los escenarios matemáticos que explicamos en la Sección 1.5.
Hay sistemas de firma de grupo basados en RSA [2], en la dificultad del problema de logaritmo discreto [14], más eficientes usando las propiedades de los emparejamientos bilineales [30] y con seguridad post-cuántica, basados en retículos euclideanos [40].
De la misma manera, hay sistemas de firma de anillo basados en RSA [50], en la dificultad del problema de logaritmo discreto [31, 35], más eficientes usando las propiedades de los emparejamientos bilineales [16] y con seguridad post-cuántica, basados en retículos euclideanos [1].
En algunas situaciones reales hay que almacenar y verificar muchas firmas digitales, posiblemente provenientes de diferentes firmantes y correspondientes a diferentes mensajes. Por ejemplo, en el protocolo de telecomunicaciones BGP (de Border Gateway Protocol), cada nodo intermedio recibe un paquete firmado por los nodos anteriores, verifica la validez de todas las firmas anteriores, añade su firma digital al paquete recibido y envía el resultado al nodo siguiente. Por tanto, el nodo número i tiene que verificar i − 1 firmas digitales, de i − 1 usuarios (nodos) diferentes, calculadas sobre i − 1 mensajes diferentes (porque cada mensaje es igual al anterior más una firma digital).
La solución inmediata a este problema es concatenar todas las firmas digitales y
verificarlas todas, una a una, usando cada mensaje y la clave pública de cada
firmante. La idea de las firmas agregadas es encontrar soluciones más
eficientes: dada una lista de n mensajes firmados por n usuarios, es decir,
dada una lista de n tripletas {(mi,σi, pki)}1≤i≤n, ¿existen maneras de
agregar las n firmas en una firma única, es decir sustituir {(mi,σi, pki)}1≤i≤n
por 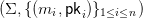 , de manera que verificar la validez de la firma
agregada Σ sea más rápido que verificar una a una la validez de todas las
σi?
, de manera que verificar la validez de la firma
agregada Σ sea más rápido que verificar una a una la validez de todas las
σi?
Además de ese objetivo de ganar en eficacia a la hora de verificar varias firmas, un sistema de agregación de firmas debe ser seguro: quién verifique una firma agregada Σ tiene que estar convencido de que proviene de n firmas individuales válidas, aunque nunca llegue a ver esas firmas σi. Es decir, la única manera de generar una firma agregada Σ válida para n parejas de mensaje / usuario {(mi, pki)}1≤i≤n es conocer, para cada índice i, o bien la clave secreta ski, o bien una firma válida σi para el mensaje mi bajo la clave pública pki.
Además de protocolos de telecomunicaciones atravesando varios nodos, como hemos visto anteriormente en el caso de BGP, las firmas agregadas pueden aplicarse en otras situaciones. Describimos brevemente a continuación un par de ejemplos.
- Cadena de bloques (blockchain): es un paradigma, un modelo de computación distribuida muy útil para llegar a consensos sin la presencia de autoridades de confianza. Apareció por primera vez en el contexto de las cripto-monedas (como bitcoin) pero en los últimos años su uso se ha extendido a otras aplicaciones, por ejemplo la firma de contratos.
La idea de blockchain es que se van creando cadenas de paquetes: cada paquete lo genera y agrega un usuario potencialmente diferente, a una cadena con la que el paquete esté relacionado. Para añadir autenticación e integridad a esas bases de datos distribuidas, se pueden firmar digitalmente los paquetes almacenados (con firmas estándar, o con firmas anónimas de grupo/anillo). Para verificar la validez de una cadena, por tanto, habría que verificar todas las firmas de todos los paquetes que formen la cadena. Un sistema de firmas agregadas puede hacer que esa verificación sea más eficiente, y que sólo haya que almacenar la firma agregada de la cadena, que idealmente ocupa (mucha) menos memoria que almacenar todas las firmas individuales de cada paquete.
- Sistemas de contaje de visitas a una página web. Algunas empresas pagan a páginas web para insertar publicidad de su empresa en ellas. La cantidad de dinero que pagan depende de las visitas que reciba esa página web. Por tanto, el propietario de la página web debe poder demostrar a la empresa que ha recibido un número determinado x de visitas en el mes actual, por ejemplo. Una manera de hacerlo es requerir que los usuarios que visitan la página web firmen digitalmente un determinado mensaje, m = (web W,mes M,código C). Cuando la página web haya recibido x visitas y por tanto recogido x firmas digitales de ese mensaje, provenientes de x usuarios diferentes, en vez de enviar todas las firmas a la empresa de publicidad, lo que puede hacer es usar un sistema de firma agregada para agregar todas las firmas en una firma más corta, que pueda ser verificada de manera más eficiente por la empresa que se publicita.
Debido a las propiedades de seguridad de las firmas agregadas, si la verificación es correcta la empresa estará convencida que los x usuarios efectivamente han firmado el mensaje y por tanto han accedido a la página web (que es donde estaba el mensaje m a firmar).
Entre los sistemas de firma agregada propuestos en la literatura, se pueden distinguir dos tipos: los sistemas de agregación secuencial y los sistemas de agregación libre. En los primeros, las firmas se van agregando siguiendo un orden concreto, y ese orden también debe ser conocido por el verificador de la firma agregada. En los sistemas de segundo tipo, no existe esa restricción: las firmas pueden agregarse y verificarse sin seguir ningún orden concreto (posiblemente operándolas todas a la vez).
Para algunas aplicaciones, como el protocolo BGP o algunos usos específicos del blockchain, las firmas agregadas secuenciales pueden ser suficientes. Para otras aplicaciones, como el sistema de contaje de visitas a una página web, es mejor que el sistema de agregación empleado sea libre.
Los únicos sistemas de agregación libre realmente eficientes propuestos en la literatura funcionan en el escenario matemático de los emparejamientos bilineales [12]. En cambio, para sistemas de agregación secuencial, hay otras propuestas que funcionan en otros escenarios, por ejemplo en el escenario post-cuántico basado en retículos euclideanos [4] o bien esquemas genéricos basados en permutaciones unidireccionales con trampa (por ejemplo la función RSA) [41].