Informe 
sobre protocolos criptográficos
sobre protocolos criptográficos
¿Qué quiere decir que un protocolo criptográfico sea seguro? La respuesta a esta pregunta dependerá del tipo de protocolo criptográfico, y posiblemente haya varias respuestas posibles, cada una correspondiente a un nivel de seguridad deseado (de más débil a más fuerte).
Por ejemplo, consideremos una aplicación de cifrado de mensajes electrónicos: si un usuario A quiere enviar un mensaje m cifrado a un usuario B, la aplicación calcula un valor cifrado c = Enc(m,A,B) y lo envía por correo electrónico (a través de un canal posiblemente público) al usuario B, quién ejecuta una función de descifrado para recuperar m = Dec(c,A,B). Posiblemente alguna de esas dos funciones necesiten recibir como entrada las claves públicas y/o privadas de A y/o de B. Puesto que el canal por el que viaja el valor c es público, un primer nivel de seguridad parece obvio: un atacante (es decir, un usuario diferente de B) que obtenga el valor c no debe ser capaz de recuperar el mensaje escondido, m. Pero, ¿qué pasa si el atacante encuentra la manera de determinar, no todo el mensaje escondido m, pero sí el valor del último bit de m? No sería un ataque tan poderoso como recuperar el mensaje m en su totalidad, pero podría tener consecuencias no deseadas, por ejemplo si el último bit de m contiene la respuesta, “sí” o “no”, a una pregunta privada.
También se pueden considerar situaciones diferentes en función de cuántos usuarios estén enviándose mensajes, si sus claves están relacionadas o no, cuántos mensajes cifrados y cuántos mensajes en claro puede obtener el atacante, etc. Por último, es imprescindible tener en cuenta cuáles son los recursos computacionales y temporales de los que dispone el atacante: ¿tiene capacidad de cálculo y tiempo ilimitados? o bien ¿dispone de una cantidad de tiempo limitada y de una capacidad de cálculo estándar, por ejemplo la proporcionada por un ordenador? o incluso ¿dispone el atacante de un ordenador cuántico?
A la vista de tantas situaciones posibles, es obvio que la respuesta a la pregunta inicial no es fácil ni única. Se tratará pues de fijar un modelo de seguridad concreto para el protocolo criptográfico concreto que estemos analizando. El modelo de seguridad definirá cuáles son los recursos disponibles para un atacante, y cuál es su objetivo final. Después, diremos que el protocolo es seguro en ese modelo si podemos demostrar que es imposible que un atacante tenga éxito al intentar romper el protocolo en ese modelo de seguridad.
Aquí hay que detenerse para comentar el significado de las palabras “imposible” y “demostrar” en el párrafo anterior. En la gran mayoría de protocolos criptográficos modernos, la seguridad no es absoluta: primero, se consideran atacantes con limitaciones de tiempo y capacidad de cálculo (lo que se conoce como atacantes en tiempo polinómico); segundo, no se demuestran resultados absolutos del tipo:
“Ningún atacante en tiempo polinómico puede romper este protocolo criptográfico en este modelo de seguridad”.
Lo que se demuestra son resultados relativos: relaciones entre la dificultad de romper el protocolo criptográfico y la dificultad de romper algún otro problema (en general, de matemáticas o de teoría de la computación) como por ejemplo el problema de factorizar un número entero muy grande. Es decir, un resultado de seguridad típico en criptografía moderno podría tener el aspecto siguiente:
“Si un atacante en tiempo polinómico t pudiese romper este protocolo criptográfico en este modelo de seguridad, entonces sería posible factorizar un número entero de tamaño 2t en tiempo polinómico en t”.
Por tanto, la seguridad del protocolo criptográfico se basa en la (hipotética) dificultad de un problema matemático concreto. En el ejemplo anterior, puesto que no se conoce ninguna manera de factorizar enteros de tamaño 2t en tiempo polinómico en t, la conclusión sería que el protocolo criptográfico resiste la acción de atacantes en tiempo polinómico, en ese modelo de seguridad.
El objetivo de la criptografía es proporcionar algunas propiedades de seguridad a las comunicaciones digitales. Ejemplos de dichas propiedades pueden ser la confidencialidad, la autenticación, el no repudio, el anonimato o la robustez. Algunas de esas propiedades pueden ser (parcialmente) incompatibles entre si, como el no repudio y el anonimato.
Para obtener esas propiedades, hace falta utilizar una o varias funcionalidades criptográficas. A grandes rasgos, el cifrado proporciona confidencialidad, la firmas digitales (y algunas de sus variantes) proporcionan autenticación, no repudio y anonimato, y las pruebas de conocimiento proporcionan robustez: es posible detectar si un usuario está efectuando las operaciones criptográficas de manera correcta.
Al ser el último tipo de funcionalidad, las pruebas de conocimiento, el más técnico, específico y trasversal, hemos decidido no considerarlo en este informe; nos centraremos en las funcionalidades relacionadas con el cifrado y la firma digital. Esta elección también puede interpretarse de otra manera: consideraremos usuarios potencialmente curiosos (es decir, posibles ataques que quieran romper la confidencialidad, la autenticación o el anonimato) pero honestos (es decir, los usuarios siempre ejecutan los protocolos criptográficos correspondientes de manera correcta). Las pruebas de conociemiento son una capa adicional de seguridad que se puede añadir a este nivel, y que permite resistir también la acción de usuarios deshonestos que se desvían del protocolo criptográfico.
El lector interesado en las pruebas de conocimiento puede obtener más información sobre ellas a partir del enlace correspondiente, en la Sección 5. Para un uso concreto de pruebas de conocimiento, se puede consultar el informe sobre votación electrónica, disponible en la página web del proyecto eSAMCid.
La estructura de un sistema básico de cifrado y la de un sistema básico de firma son bastante parecidas. En los dos casos hay un protocolo de generación de claves, KG, que toma como entrada el nivel de seguridad deseado (por ejemplo, la longitud de las claves secretas que se considera suficientemente segura) y da como salida unas claves criptográficas para cada usuario. En el caso de un sistema de cifrado, siguen dos protocolos más: el protocolo de cifrado en si mismo, Enc, que toma como entrada una clave k1 y un texto en claro m y da como salida un texto cifrado c, lo escribimos Enc(k1,m) → c; y el protocolo de descifrado, que toma como entrada un texto cifrado c y una clave k2, y da como salida un texto en claro m, lo escribimos Dec(k2,c) → m. En el caso de firma, siguen al protocolo de generación de claves dos protocolos diferentes, uno para firmar el mensaje, Sign y otro para verificar que una firma es correcta, Vfy. Análogamente al caso del cifrado, escribiremos Sign(k3,m) → σ y Vfy(k4,σ,m) → 1 (firma válida) o 0 (firma no válida), donde k3 es la clave de firma y k4 es la correspondiente clave de verificación.
Existen dos posibles escenarios para un protocolo criptográfico, según el tipo de claves criptográficas que poseen los usuarios que se están comunicando entre si.
Los protocolos de cifrado y de firma que funcionan en un entorno de clave simétrica son (mucho) más eficientes que los que veremos en el segundo escenario. Algunos ejemplos son DES y AES para cifrado, o sistemas de firma simétrica (en inglés, Message Authentication Codes, MACs) que están basados en funciones hash.
En cambio, el escenario de clave simétrica tiene dos inconvenientes bastante evidentes. Por un lado, un usuario A debe compartir al menos una clave secreta kAB con cada otro usuario B con el que vaya a comunicarse. En muchas aplicaciones de la vida real (por ejemplo, el correo electrónico), el número de usuarios es muy grande, y por tanto mantener tantas claves secretas es inviable. Por otro lado, no es nada trivial cómo dos usuarios A y B pueden acordar una clave secreta común, kAB, sin que el resto de usuarios la conozca, en un entorno de comunicación digital donde por ejemplo A y B no pueden encontrarse físicamente de manera segura. Este problema se conoce como el problema del acuerdo de clave (en inglés, key agreement). El objetivo de la criptografía asimétrica, inventada en 1976 por Diffie y Hellman [19], fue precisamente minimizar estos dos problemas de la criptografía simétrica.
En efecto, la criptografía asimétrica resuelve los dos inconvenientes principales de la criptografía simétrica: cada usuario A puede generar sus claves de manera individual, sin interactuar con otros usuarios; y A tiene que almacenar en privado sólo una clave secreta, skA, independientemente del número de usuarios con los que se vaya a comunicar.
Por otro lado, la criptografía asimétrica también tiene desventajas. Primero, para evitar ataques de suplantación de identidad (en inglés, man in the middle attacks), el sistema tiene que disponer de autoridades de certificación que den fe que una clave pública pkA pertenece realmente al usuario A. Segundo, diseñar protocolos específicos en este entorno asimétrico es más difícil que en el entorno simétrico, puesto que un atacante tiene más información (todas las claves públicas de todos los usuarios) que en el entorno simétrico. Por ejemplo, debe ser imposible poder obtener skA a partir de pkA y además estas claves deben ser compatibles después con operaciones de cifrado, descifrado, firma y verificación, o sea que tienen que tener una estructura matemática más rica que en la criptografía simétrica. En la práctica, esto se traduce en el uso de funciones matemáticas que sean fáciles de calcular pero muy difíciles de invertir; el primer candidato fue el sistema RSA, propuesto en 1978. Para que un atacante no pueda invertir esas funciones matemáticas en tiempo polinómico, los números implicados (las claves secretas y públicas) tienen que ser muy grandes, y por tanto las operaciones de cifrar, descifrar, firmar, etc. se hacen más ineficientes que en el escenario de la criptografía simétrica.
En muchas aplicaciones de la vida real, lo que se hace es combinar los dos escenarios, para intentar retener las mejores propiedades de cada uno de ellos. Es lo que se conoce como criptografía híbrida: si dos usuarios A y B van a iniciar una comunicación, se usa el escenario de clave pública para generar las claves individuales, (skA, pkA) para A y (skB, pkB) para B, y luego se usa una ronda de comunicación (secreta y autenticada mediante cifrado más firma) de clave pública entre ellos para acordar de manera privada una clave común kAB. A partir de ese momento, para el resto de mensajes que se intercambien A y B, pueden usar protocolos criptográficos simétricos con la clave secreta común kAB, consiguiendo mucha más eficiencia en las comunicaciones posteriores.
En los últimos años, con la aparición de nuevas y más complejas formas de comunicación digital en la vida real, se han propuesto otros escenarios criptográficos diferentes a los que hemos visto en el apartado anterior, el de criptografía simétrica y el de criptografía asimétrica.
Uno de estos nuevos escenarios es el de la criptografía basada en identidades, que nació con el objetivo de minimizar uno de los problemas de la criptografía asimétrica: la necesidad de certificados digitales que vinculen la identidad del usuario A con su clave pública pkA. La solución propuesta por la criptografía basada en identidades es que la clave pública pkA de un usuario A sea directamente algún elemento único de su identidad, como puede ser un número de documento de identidad, un número de teléfono, una dirección de correo electrónico... algo que todo el mundo pueda asociar de manera inequívoca con el usuario A, sin necesidad de una autoridad que lo certifique. Pero el problema entonces es: ¿quién y cómo genera una clave secreta skA asociada a esa clave pública pkA ≈ idA? La función que calcule skA a partir de idA debe involucrar algún tipo de información secreta, porque de lo contrario cualquiera podría ejecutarla y obtener la clave secreta skA de cualquier usuario A, a partir de su identidad (pública) idA. La solución propuesta consiste en disponer de autoridades máster, terceras partes de confianza que usan sus propias claves secretas para calcular skA a partir de idA y enviar skA a A de manera segura.
Por tanto, el precio a pagar para evitar la necesidad de gestión de certificados digitales es la necesidad de terceras partes de confianza que generan (y por tanto conocen) las claves secretas de todos los usuarios del sistema. Con sus ventajas e inconvenientes, la criptografía basada en identidades puede ser una solución muy interesante para las comunicaciones digitales por ejemplo dentro de una organización jerarquizada.
Una característica común de los tres entornos criptográficos que hemos visto hasta ahora (simétrico, asimétrico y basado en identidades) es que cada operación criptográfica está muy ligada a un usuario individual concreto, el que hemos denominado A. Por ejemplo, un sistema de cifrado se usa para enviar un mensaje a A de manera confidencial, ya sea usando kAB, pkA o idA a la hora de ejecutar el protocolo de cifrado Enc. De manera análoga, una firma la calcula A y su validez se verifica usando la información específica de A, para llegar a la conclusión que ha sido efectivamente el usuario individual A quién ha firmado el mensaje.
Podemos considerar situaciones más generales en las que se cifra un mensaje con la idea que más de un usuario tenga la capacidad de descifrar el texto cifrado y recuperar el mensaje en claro, posiblemente sin saber exactamente la lista concreta de usuarios que tienen o tendrán esa capacidad. Por ejemplo, cifrar una base de datos médicos, resultante de algún ensayo clínico, de manera que sólo puedan descifrar aquellos usuarios que sean o bien médicos del hospital H1 o bien empleados de la casa farmacéutica F2 o bien directores de los hospitales afiliados H3,H4,H5. Esta situación sería un ejemplo de cifrado basado en atributos, que es un caso particular (igual que la criptografía basada en identidades) de lo que se conoce como criptografía funcional: la capacidad de un usuario A para poder efectuar una operación criptográfica secreta (como descifrar o firmar) dependerá de si los atributos xA del usuario A satisfacen alguna condición y impuesta por la persona que ha cifrado o firmado el mensaje, es decir, si se cumple f(xA,y) = 1 para alguna relación booleana concreta f.
La criptografía funcional está recibiendo mucha atención por parte de la comunidad criptográfica internacional en los últimos años, debido a sus múltiples aplicaciones en situaciones reales (control de acceso, delegación de cálculos costosos, almacenaje seguro en la Nube, etc.). Detallamos un poco más algunas de estas aplicaciones en la Sección 4.
La gran parte de los protocolos criptográficos concretos que se han propuesto en los últimos años y que se usan en la vida real, y en el caso de la criptografía asimétrica y funcional, todos ellos, se basan en el uso de objetos y operaciones matemáticas que tengan (hipotéticamente) propiedades interesantes desde el punto de vista criptográfico. Por ejemplo, como hemos comentado anteriormente, para poder implementar un sistema de cifrado de clave pública, se necesitan funciones c = Enc(pkA,m) que se puedan calcular de manera eficiente, pero que sean muy difíciles (computacionalmente imposibles) de invertir, para que un atacante diferente de A no pueda recuperar el mensaje en claro m a partir de c; a la vez, la función debe poder invertirse de alguna manera si se conoce el valor de la clave secreta skA, para que el usuario A sí que pueda descifrar y recuperar m. En resumen, se necesitan funciones unidireccionales con trampa.
Se han propuesto diferentes entornos matemáticos que se pueden usar para diseñar protocolos criptográficos concretos, con las propiedades de seguridad deseadas, basándose en la dificultad computacional de resolver algún problema matemático asociado a cada uno de esos entornos. Repasamos a continuación cuatro de esos entornos, posiblemente los más conocidos y usados.
La primera candidata concreta a función unidireccional con trampa fue la función RSA propuesta por Rivest, Shamir y Adleman en 1978 [49], basada en la idea de que factorizar números grandes es muy difícil.
En concreto, si N = p⋅q es el producto de dos números primos (cada uno con λ∕2 bits de longitud), entonces no se conoce ningún algoritmo eficiente (es decir, en tiempo polinómico en λ) que encuentre la factorización de N dado sólo N como dato. Es lo que se conoce como el problema de la factorización. Si usamos la notación ℤN = {0, 1,…,N − 1}, entonces hay otros problemas que se suponen difíciles computacionalmente (sin solución polinómica a día de hoy) y que están relacionados con el problema de la factorización (todos se podrían resolver a partir de la solución del problema de la factorización). Aquí van algunos ejemplos:
La seguridad de muchos protocolos criptográficos se basa en estos problemas, incluyendo el cifrado y la firma RSA [49], el cifrado de Goldwasser-Micali [28], el cifrado de Paillier [43], la firma y el cifrado de Rabin [47], etc.
Dado un grupo finito cíclico de orden primo p, es decir 𝔾 = ⟨g⟩ = {1,g,g2, …,gp−1}, donde el número primo p tiene λ bits de longitud, no se conoce ningún algoritmo eficiente y general (que funcione en cualquier grupo 𝔾 y emplee tiempo polinómico en λ) para resolver el problema del logaritmo discreto: dados p, 𝔾,g y un elemento aleatorio y ∈ 𝔾, encontrar el número x ∈ ℤp = {0, 1,…,p − 1} tal que y = gx.
Hay otros dos problemas que se pueden definir en este tipo de grupos, y que también se consideran intratables computacionalmente a día de hoy (aunque ambos podrían resolverse si se resolviese el problema del logaritmo discreto):
Algunos ejemplos de criptosistemas cuya seguridad se basa en la dificultad computacional de resolver estos los problemas mencionados son los cifrados de ElGamal [22] o Cramer-Shoup [18], el intercambio de claves de Diffie-Hellman [19], o el sistema de firma de Schnorr [53].
Usando herramientas sofisticadas de teoría de números y curvas elípticas, se pueden encontrar ejemplos de tripletas de grupos finitos cíclicos, 𝔾1, 𝔾2, 𝔾T , todos con el mismo orden primo p, que admitan un emparejamiento bilineal no-degenerado: es decir, una aplicación e : 𝔾1 × 𝔾2−→𝔾T tal que, si 𝔾1 = ⟨g1⟩ y 𝔾2 = ⟨g2⟩, se verifique
Algunos ejemplos son el emparejamiento de Weil, el de Tate o el ate. Usando las propiedades algebraicas de estos emparejamientos, se pueden diseñar protocolos criptográficos mucho más eficientes (por ejemplo el sistema de firma BLS [13]) y también se encuentran soluciones para algunas funcionalidades (como la criptografía basada en identidades o en atributos, dentro de la criptografía funcional) para las que no se conoce/conocía solución en otros escenarios más clásicos, como el de factorización o logaritmo discreto.
Para demostrar la seguridad de los protocolos propuestos en un escenario de emparejamiento bilineal, además de asumir la dificultad del problema del logaritmo discreto en cada uno de los grupos, a menudo hay que basarse en la seguridad de algún otro problema específico de este escenario. Un par de ejemplos:
Todos los problemas computacionales relacionados con los diferentes entornos matemáticos que hemos visto hasta ahora tienen un inconveniente: se pueden resolver de manera eficiente (en tiempo polinómico en la longitud de las claves λ) con un ordenador cuántico, a través del ataque propuesto por Shor. A día de hoy, no se dispone aún de ordenadores cuánticos suficientemente potentes y polivalentes para llevar a cabo ese ataque, pero la investigación en ese ámbito avanza, y no es descabellado suponer que algún día no muy lejano existirán ordenadores cuánticos donde se pueda ejecutar el ataque de Shor y que permitan, por tanto, factorizar enteros o calcular logaritmos discretos de manera eficiente.
Cuando llegue ese día, todos los criptosistemas cuya seguridad se basa en los problemas computacionales de los tres escenarios anteriores dejarán de ser seguros automáticamente. Por eso, la comunidad criptográfica también trabaja en proponer otros protocolos criptográficos que utilicen herramientas matemáticas diferentes, de manera que se pueda basar su seguridad en la dificultad de romper otros problemas computacionales que resistan el ataque de un ordenador cuántico. Se dice entonces que estos protocolos tienen seguridad post-cuántica. Entre estos nuevos escenarios para proporcionar seguridad post-cuántica, el que está recibiendo más atención y generando más resultados (algunos sorprendentes) es el de la criptografía basada en retículos (en inglés, lattice-based cryptography).
Un retículo euclideano de dimensión n es un subgrupo de ℝn que es isomórfico a ℤn. Es decir, un retículo Λ ⊂ ℝn tiene la forma
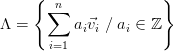
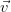1,…,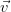
n} de ℝn. Es decir, son las combinaciones lineales,
con coeficientes enteros, de los vectores de esa base. Los vectores de la base
puede que no tengan coeficientes enteros. Un ejemplo en ℝ2, tomando
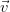1 = (0,
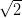) y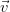 
2 = (1, 0), el retículo generado por esa base contendría puntos
como el (3,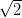
) o el (−2,−
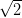), pero no contendría ningún punto cuyas dos
coordenadas fuesen números enteros.
Cuando n es un número bastante grande (mayor a 100, por ejemplo), algunos problemas matemáticos se consideran computacionalmente intratables, es decir que no se conoce ningún algoritmo que funcione en tiempo polinómico en n y los resuelva, ni siquiera usando un ordenador cuántico. Un par de esos problemas son:
Además, hay otros problemas matemáticos relacionados con sistemas de ecuaciones lineales con coeficientes enteros a las que se le añade un ruido (un número elegido según una distribución gaussiana discreta de probabilidad), que en principio no parecen relacionados con el mundo de los retículos, pero que se puede demostrar que son al menos tan difíciles de resolver como alguno de los problemas anteriores, definidos en retículos.
Sin entrar en definir de manera formal ninguno de estos problemas, sí que podemos mencionar algunos, como el problema de encontrar soluciones pequeñas de sistemas ecuaciones (SIS, Short Integer Solution) o bien el problema de aprendizaje con errores (LWE, Learning With Errors). El lector interesado en profundizar en estos conceptos de la criptografía basada en retículos, puede consultar Wikipedia o bien, como referencia más formal pero tal vez más difícil de leer, el tutorial [45].
Algunos ejemplos de protocolos criptográficos con seguridad post-cuántica, basados en retículos euclideanos, son el sistema de cifrado de Regev [48], los sistemas de firma de Lyubashevsky [42], los sistemas NTRU tanto para cifrar como para firmar [36, 37], y los protocolos de cifrado completamente homomórficos (empezando por el original de Gentry [27]), que supusieron una auténtica revolución en el mundo de la criptografía. También hay protocolos criptográficos basados en retículos para diferentes tipos de criptografía funcional, incluyendo la basada en identidades y la basada en atributos.
