Largest Known (Degree, Diameter)-Graphs

Diameter 6

Last modification: June 22, 2025.
http://www-mat.upc.es/grup_de_grafs/desc_g.html
row adjacency list format: the first vertex of each row is adjacent to all the other vertices in that row.
implicit adjacency list format: each row corresponds to a vertex (row 1, vertex 0; row 2, vertex 1; and so on) and contains all vertices adjacent to it.
adjacency list NX NetworkX format. NetworkX format.
Exoo_132
Delta= 3, Diam= 6; N=132; Moore bound=190;
Ord.: 132 / Size: 198 / 3-reg. / Diam.: 6 / Girth: 6 / Avg.dist: 4.72149 / Alg.conn. 0.437172 / Domin. number: 35 / Aut.group.ord.: 2 / k-cycles for k= 3 up to 14: (0, 0, 0, 1, 2, 0, 4, 12, 16, 676, 396, 676)
Details of this construction at: Geoffrey Exoo. A family of graphs and the degree/diameter problem.  J. Graph Theory 37 (2001), 118-124.
Communicated by G. Exoo (May 22, 1998). G.E. data
Download the implicit adjacency list of the graph.
Download the NX adjacency list of the graph.
--------------------
Other non-isomorphic instances, several with a lower average distance, larger girth and automorphism groups, found by F.Comellas (2025)
  1. Ord.: 132 / Size: 198 / 3-reg. / Diam.: 6 / Girth: 5 / Avg.dist: 4.72415 / Alg.conn. 0.415114 / Dom.num.: 36 / Aut.group.ord.: 4 / k-cycles for k= 3 up to 14: (0, 0, 3, 0, 0, 0, 0, 0, 24, 708, 348, 726). G1 132 adjlist NX
  2. Ord.: 132 / Size: 198 / 3-reg. / Diam.: 6 / Girth: 5 / Avg.dist: 4.72276 / Alg.conn. 0.419280 / Dom.num.: 36 / Aut.group.ord.: 4 / k-cycles for k= 3 up to 14: (0, 0, 2, 0, 1, 0, 2, 4, 20, 698, 364, 710). G2 132 adjlist NX
  3. Ord.: 132 / Size: 198 / 3-reg. / Diam.: 6 / Girth: 5 / Avg.dist: 4.72137 / Alg.conn. 0.422815 / Dom.num.: 35 / Aut.group.ord.: 2 / k-cycles for k= 3 up to 14: (0, 0, 1, 0, 2, 0, 4, 8, 16, 688, 380, 694). G3 132 adjlist NX
  4. Ord.: 132 / Size: 198 / 3-reg. / Diam.: 6 / Girth: 7 / Avg.dist: 4.71536 / Alg.conn. 0.444035 / Dom.num.: 36 / Aut.group.ord.: 4 / k-cycles for k= 3 up to 14: (0, 0, 0, 0, 3, 0, 6, 4, 20, 706, 356, 706). G4 132 adjlist NX
  5. Ord.: 132 / Size: 198 / 3-reg. / Diam.: 6 / Girth: 7 / Avg.dist: 4.71999 / Alg.conn. 0.444035 / Dom.num.: 35 / Aut.group.ord.: 4 / k-cycles for k= 3 up to 12: (0, 0, 0, 0, 3, 0, 6, 12, 12, 678, 396, 678). G5 132 adjlist NX
  6. Ord.: 132 / Size: 198 / 3-reg. / Diam.: 6 / Girth: 7 / Avg.dist: 4.71999 / Alg.conn. 0.444035 / Dom.num.: 35 / Aut.group.ord.: 12 / k-cycles for k= 3 up to 14: (0, 0, 0, 0, 3, 0, 6, 12, 12, 678, 396, 678). G6 132 adjlist NX
  7. Ord.: 132 / Size: 198 / 3-reg. / Diam.: 6 / Girth: 7 / Avg.dist: 4.71999 / Alg.conn. 0.444035 / Dom.num.: 35 / Aut.group.ord.: 6 / k-cycles for k= 3 up to 14: (0, 0, 0, 0, 3, 0, 6, 12, 12, 678, 396, 678). G7 132 adjlist NX
  8. Ord.: 132 / Size: 198 / 3-reg. / Diam.: 6 / Girth: 7 / Avg.dist: 4.71443 / Alg.conn. 0.423029 / Dom.num.: 36 / Aut.group.ord.: 4 / k-cycles for k= 3 up to 14: (0, 0, 0, 0, 1, 0, 10, 10, 16 , 697, 360, 710 ). G8 132 adjlist NX
  9. Ord.: 132 / Size: 198 / 3-reg. / Diam.: 6 / Girth: 5 / Avg.dist: 4.72415 / Alg.conn.0.419280 / Dom.num.: 36 / Aut.group.ord.: 12 / k-cycles for k= 3 up to 14: (0, 0, 3, 0, 0, 0, 0, 0, 24, 708, 348, 726 ). G9 132 adjlist NX
This SageMath script, computes several of their properties. This is the online version .
--------------------
H3(K3)
Delta= 4, Diam= 6; N=740; Moore bound=1457;
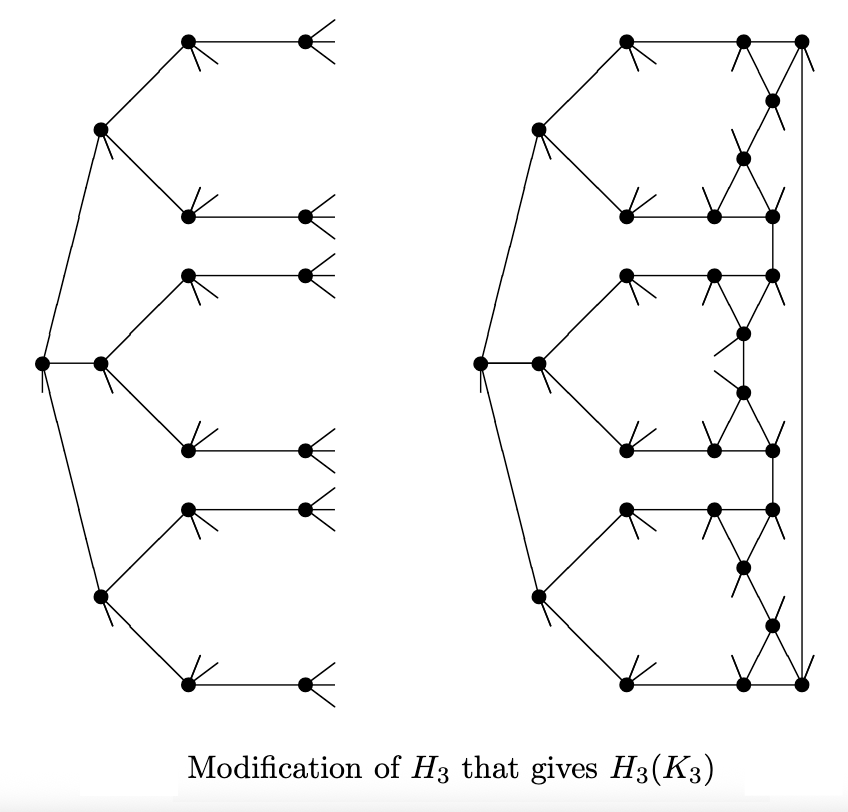Graph obtained from the generalized hexagon H3 by replacement of some of its vertices (see figure) by complete graphs K3
F. Comellas and J. Gómez, New large graphs with given degree and diameter.,
Graph Theory, Combinatorics and Algorithms, vol 1, Yousef Alavi and Allen Schwenk (Eds.), John Wiley & Sons, Inc.; New York (1995) pp. 221-233. ISBN 0-471-30437-9.
(Proc. of the Seventh Quadrennial International Conference on the Theory and Applications of Graphs, Kalamazoo, MI, USA, June 1992.)
Download the NX adjacency list of H3(K3) or/and the NX adjacency list of H3 (the generalized hexagon H3, base of the former graph)
This SageMath script , constructs H3(K3) from H3 and computes several of their properties. This is the online version .
H4(K3)
Delta= 5, Diam= 6; N=2 772; Moore bound=6826;
Graph obtained from the generalized hexagon H4 by replacement of some of its vertices by complete graphs K3 using the same technique than in reference (4,6)
G. Pineda-Villavicencio, J. Gómez, M. Miller, H. Pérez-Rosés. New largest known graphs of diameter 6. Networks 53 (2009) 315-328.
H5(K4)
Delta= 6, Diam= 6; N=7 917; Moore bound=23437;
Graph obtained from the generalized hexagon H5 by replacement of some of its vertices by complete graphs K4 using the same technique than in reference (4,6)
G. Pineda-Villavicencio, J. Gómez, M. Miller, H. Pérez-Rosés. New largest known graphs of diameter 6. Networks 53 (2009) 315-328.
Com_12264
Degree= 7, Diameter =6; Order =12264; Moore bound=65318.
Cayley graph. Found as a semidirect product, 12264 nodes and 42924 edges (F.Comellas 2024):
  1. Z_24 x(90) Z_511, generators [13,77]<>[11,245]:[6,157]<>[18,214]:[15,50]<>[9,281]:[12,7]<>[12,7]. Avg. dist.: 5.197423 (1,7,42,252,1463,5957,4542) transmission: 63736. adjlist NX
  2. Z_24 x(125) Z_511, generators [9,122]<>[15,52]:[19,168]<>[5,70]:[18,254]<>[6,369]:[12,231]<>[12,231]. Avg. dist.: 5.197423 (1,7,42,252,1463,5957,4542) transmission: 63736. adjlist NX
  3. Z_24 x(139) Z_511, generators [18,219]<>[6,292]:[9,373]<>[15,30]:[5,467]<>[19,152][12,252]<>[12,252]. Avg. dist.: 5.197423 (1,7,42,252,1463,5957,4542) transmission: 63736. adjlist NX
  4. Z_24 x(153) Z_511, generators [6,206]<>[18,424]:[7,30]<>[17,72]:[3,437]<>[21,136]:[12,266]<>[12,266]. Avg. dist.: 5.197423 (1,7,42,252,1463,5957,4542) transmission: 63736. adjlist NX
  5. Z_24 x(167) Z_511, generators [7,62]<>[17,111]:[3,413]<>[21,399]:[6,410]<>[18,339]:[12,119]<>[12,119]. Avg. dist.: 5.197423 (1,7,42,252,1463,5957,4542) transmission: 63736. adjlist NX
  6. Z_24 x(202) Z_511, generators [23,321]<>[1,55]:[21,488]<>[3,5 ]:[18,192]<>[6,74]:[12,469]<>[12,469]. Avg. dist.: 5.197423 (1,7,42,252,1463,5957,4542) transmission: 63736. adjlist NX
  7. Z_24 x(335) Z_511, generators [18,116]<>[6,80]:[13,13]<>[11,440]:[15,383]<>[9,250]:[12,21]<>[12,21]. Avg. dist.: 5.197423 (1,7,42,252,1463,5957,4542) transmission: 63736. adjlist NX
  8. Z_24 x(468) Z_511, generators [23,219]<>[1,219]:[18,2]<>[6,19]:[21,12]<>[3,47]:[12,35]<>[12,35]. Avg. dist.: 5.197423 (1,7,42,252,1463,5957,4542) transmission: 63736. adjlist NX

All graphs are isomorphic.
Former result, Order = 11988
Communicated by Eyal Loz, Math Dep., Auckland Univ., New Zealand (July 2006)
Voltage graph Z_36 x(2) Z_333, B(0,3), voltages [(18,108)|(14,61)(34,195)(23,14)], avg. dist.: 5.1779431
Z_m x(a) Z_n represents a semidirect product of cyclic groups [x,y][u,v]= [x + u mod m, y*a^u + v mod n].
( raw adjacency list from Loz ) ::: Link to Eyal Loz's original data. --- adjlist NX version.

Found also as a semidirect product (no voltages), some instances have a lower average distance (F.Comellas 2024):
Z_36 x(5)Z_333 with generators [26,80]<>[10,301] : [14,3]<>[22,321] : [1,60]<>[35,321] :[18,324] and their inverses. Avg. dist. 5.177943 adjlist NX
Z_36 x(56)Z_333 with generators [14,2]<>[22,310]:[34,72]<>[2,315]:[31,113]<>[5,326]:[18,324] and their inverses. Avg. dist. 5.180195 adjlist NX
Z_36 x(59)Z_333 with generators [14,216]<>[22,279]:[1,235]<>[35,250]:[26,218]<>[10,10]:[18,99] and their inverses. Avg. dist. 5.180195 adjlist NX
H7(K5)
Delta= 8, Diam= 6; N=39 672; Moore bound=156865;
Graph obtained from the generalized hexagon H7 by replacement of some of its vertices by complete graphs K5 using the same technique than in reference (4,6)
J. Gómez. On large (D,6)-graphs. Networks 46 (2005), pp. 82-87. doi:10.1002/net.20075 .
H8(K6)
Delta= 9, Diam= 6; N=75 893; Moore bound=337042;
Graph obtained from the generalized hexagon H8 by replacement of some of its vertices by complete graphs K6 using the same technique than in reference (4,6)
G. Pineda-Villavicencio, J. Gómez, M. Miller, H. Pérez-Rosés. New largest known graphs of diameter 6. Networks 53 (2009) 315-328.
H9(K6)
Delta= 10, Diam= 6; N=134 690; Moore bound=664301;
Graph obtained from the generalized hexagon H9 by replacement of some of its vertices by complete graphs K6 using the same technique than in reference (4,6)
J. Gómez. On large (D,6)-graphs. Networks 46 (2005), pp. 82-87. doi:10.1002/net.20075 .
H7(T4)
Delta= 11, Diam= 6; N=156864; Moore bound= 1222222 ;
H_7(T 4).
J. Gomez, M.A. Fiol. Dense Compound Graphs.Ars Combinatoria, 20-A (1985), pp. 211-237. link to the paper
H11(K8)
Delta= 12, Diam= 6; N=359 772; Moore bound=2125873;
Graph obtained from the generalized hexagon H11 by replacement of some of its vertices by complete graphs K8 using the same technique than in reference (4,6)
G. Pineda-Villavicencio, J. Gómez, M. Miller, H. Pérez-Rosés. New largest known graphs of diameter 6. Networks 53 (2009) 315-328.
H9(T4)
Delta= 13, Diam= 6; N=531440; Moore bound= 3528890;
J. Gomez, M.A. Fiol. Dense Compound Graphs.Ars Combinatoria, 20-A (1985), pp. 211-237. link to the paper
H13(K10)
Delta= 14, Diam= 6; N=816 294; Moore bound=5631277;
Graph obtained from the generalized hexagon H13 by replacement of some of its vertices by complete graphs K10 using the same technique than in reference (4,6)
G. Pineda-Villavicencio, J. Gómez, M. Miller, H. Pérez-Rosés. New largest known graphs of diameter 6. Networks 53 (2009) 315-328.
H11(T4)
Delta= 15, Diam= 6; N=1417248; Moore bound=8687926 ;
J. Gomez, M.A. Fiol. Dense Compound Graphs.Ars Combinatoria, 20-A (1985), pp. 211-237. link to the paper
H11(T5)
Delta= 16, Diam= 6; N=1771560; Moore bound= 13017857;
J. Gomez, M.A. Fiol. Dense Compound Graphs.Ars Combinatoria, 20-A (1985), pp. 211-237. link to the paper