Largest Known (Degree, Diameter)-Graphs
Diameter 4
Last modification: June 22, 2025.
https://web.mat.upc.edu/francesc.comellas/old-files/delta-d/taula_delta_d.html
raw adjacency list format: the first vertex of each row is adjacent to all the other vertices in that row.
implicit adjacency list format: each row corresponds to a vertex (row 1, vertex 0; row 2, vertex 1; and so on) and contains all vertices adjacent to it.
adjacency list NX NetworkX format. NetworkX format.
Doty, vC, AFY
Delta= 3, Diam= 4; N=38; Moore bound=46; optimal
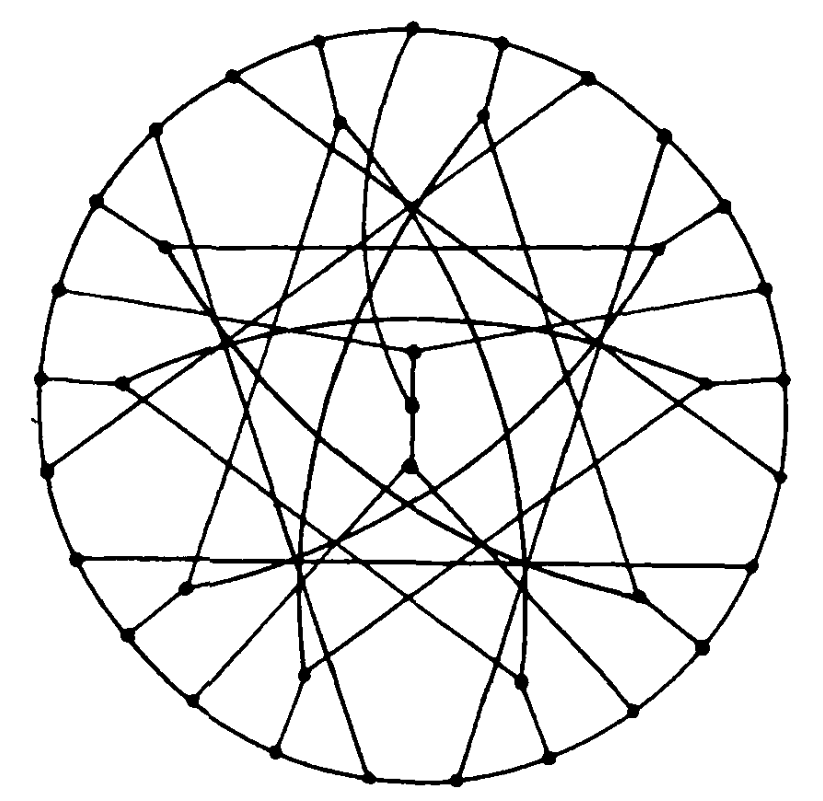
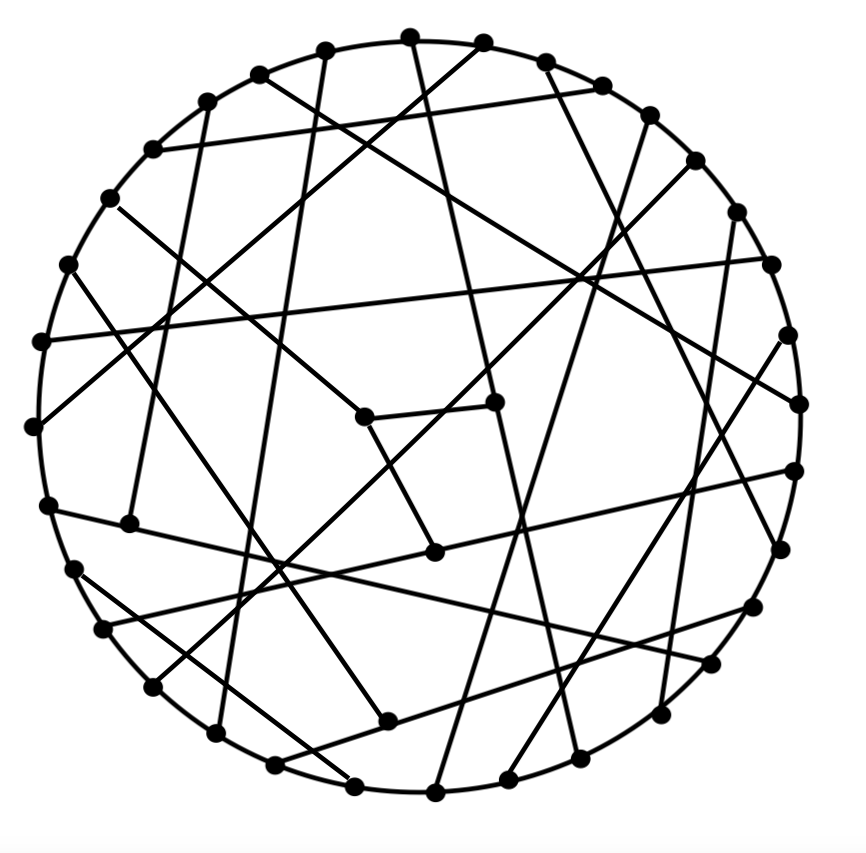 Alegre, Fiol, Yebra, von Conta graph ------- Doty graph
Alegre, Fiol, Yebra, von Conta graph ------- Doty graph
Described independently in:
- [Do82] K.W. Doty; Large regular interconnection networks;
Proc. 3rd. Int. Conf. on Distributed Computing Systems, IEEE Press, Miami, October 1982, pp. 312-317.
link to the paper (local)
- [vCo83] C. von Conta.
Torus and other networks as communication networks with up to some hundred points.
IEEE Trans Comp,c-32 (1983), pp. 657-666.
- [AlFiYe86] I. Alegre, M.A. Fiol and , J.L.A Yebra.
Some large graphs with given degree and diameter.
J. Graph Theory,10 (1986), pp.219-224.
The proof of optimality appeared in:
Dominique Buset.
Maximal cubic graphs with diameter 4. Discrete Appl. Math.101 (2000) pp. 53--61.
The graph constructed by K.W. Doty is not isomorphic to the other graphs (which are)
Download the adjacency list of the graph AFY in NetworkX format (vertices notation as in AlFiYe86).
Download the adjacency list of the graph AFY in NetworkX format (vertices labeled 0,2,...37). This graph has average distance 3.10811. Automorphism group size: 8.
More information at The House of Graphs.
Download the adjacency list of the Doty graph in NetworkX format (vertices labeled 0,2,...37). This graph has average distance 3.11664. Automorphism group size: 16.
More information at The House of Graphs.
--------------------
This SageMath script computes several properties of the graphs including symmetry group sizes and the number of k-cycles (k=3..10). This is the online version .
Exoo-98
Delta= 4, Diam= 4; N=98; Moore bound=161;
Communicated by G. Exoo (May 19, 2010).
G.E. data
Download the implicit adjacency list of the graph.
adjlist NX format
This SageMath script computes several properties of the graphs including symmetry group sizes and the number of k-cycles (k=3..). This is the online version
Exoo-212
Delta= 5, Diam= 4; N=212; Moore bound=426;
Communicated by G. Exoo (May 21, 2010).
G.E. data
Download the implicit adjacency list of the graph.
adjlist NX format
This SageMath script computes several properties of the graphs including symmetry group sizes and the number of k-cycles (k=3..). This is the online version
Loz_390
Degree= 6, Diameter = 4; Order =390; Moore
bound=937
Communicated by Eyal Loz, Math Dep., Auckland Univ., New Zealand (July 2006)
Voltage graph Z_15 x(3) Z_13, D(2,2), voltages [(2,8)<>(14,4),(0,0)<>(13,6),(9,4)<>(7,7)], avg. dist.: 3.444730
Z_m x(a) Z_n represents a semidirect product of cyclic groups [x,y][u,v]= [x + u mod m, y*a^u + v mod n].
Download the raw adjacency list of the graph.
adjlist NX format
Link to Eyal Loz's data (internet archive) .
Sa_672
Degree= 7, Diameter = 4; Order =672; Moore bound=1814
Obtained as a Cayley graph for semidirect product of Zm with Zn
Z_6*(39)Z_112 [2,73]<>[4,23], [5,54]<>[1,22], [5,71]<>[1,31], [3,42] avg.dist 3.496274
M. Sampels.
Large networks with small diameter.. In: Rolf H. Mohring (Ed.):
23rd International Workshop on Graph-Theoretic Concepts in Computer Science (WG '97), Lecture Notes in Computer Science 1335, pp. 288-302, Springer-Verlag, 1997 ISBN 3-540-63757-5. Communicated July 29, 1997
Download the raw adjacency list of the graph in NetworkX format (vertices labeled 0,2,...671) .
Other instances (F.Comellas 2024)
Z_6*(23)Z_112 [2,95]<>[4,97], [1,77]<>[5,21], [5,36]<>[1,68], [3,56] Avg.dist 3.496274 transm. 2346 adjlist NX
Z_6*(23)Z_112 [1,102]<>[5,54], [2,51]<>[4,45], [5,83]<>[1,107], [3,42] Avg.dist 3.496274 transm. 2346 adjlist NX
Z_6*(23)Z_112 [4,101]<>[2,107], [5,64]<>[1,96], [5,101]<>[1,29], [3,84] Avg.dist 3.496274 transm. 2346 adjlist NX
Z_6*(23)Z_112 [2,65]<>[4,31], [1,22]<>[5,38], [5,85]<>[1,61], [3,98] Avg.dist 3.496274 transm. 2346 adjlist NX
Z_6*(39)Z_112 [2,23]<>[4,41], [1,0]<>[5,0], [1,103]<>[5,95], [3,28] Avg.dist 3.496274 transm. 2346 adjlist NX
Z_6*(39)Z_112 [2,5]<>[4,43], [5,73]<>[1,65], [1,28]<>[5,28], [3,0] Avg.dist 3.496274 transm. 2346 adjlist NX
Z_6*(39)Z_112 [4,57]<>[2,103], [5,30]<>[1,62], [1,101]<>[5,29], [3,42] Avg.dist 3.496274 transm. 2346 adjlist NX
Z_6*(39)Z_112 [5,48]<>[1,32], [2,9]<>[4,55], [5,33]<>[1,57], [3,84] Avg.dist 3.496274 transm. 2346 adjlist NX
Loz_1100
Degree= 8, Diameter = 4; Order =1100; Moore bound=3201
Communicated by Eyal Loz, Math Dep., Auckland Univ., New Zealand (July 2006)
Voltage graph Z_20 x(2) Z_55, B(0,4), voltages [(4, 27)(12, 11)(9,9)(19, 11)], avg. dist.: 3.547771
Z_m x(a) Z_n represents a semidirect product of cyclic groups [x,y][u,v]= [x + u mod m, y*a^u + v mod n].
Download the raw adjacency list of the graph.
Link to Eyal Loz's data (internet archive) .
Found also as a semidirect product, some instances have a lower average distance (F.Comellas 2023):
Z_20 x(2) Z_55 with generators [1,45]<>[19,5]:[12,47]<>[8,13]:[11,39]<>[9,52]:[16,26]<>[4,24]. Avg. dist. 3.547771 (1,8,56,361,674) trans.: 3899 adjlist NX
Z_20 x(3) Z_55 with generators [9,8]<>[11,9]:[1,39]<>[19,42]:[8,1]<>[12,24]:[12,22]<>[8,33]. Avg. dist. 3.536852 (1,8,56,373,662) trans.: 3887 adjlist NX
Z_20 x(3) Z_55 with generators [1,33]<>[19,44]:[8,13]<>[12,37]:[9,2]<>[11,16]:[12,44]<>[8,11]. Avg. dist. 3.536852 (1,8,56,373,662) trans.: 3887 adjlist NX
Z_20 x(8) Z_55 with generators [16 9]<>[4 41]:[7 10]<>[13 50]:[17 12]<>[3 16]:[12 8]<>[8 37]. Avg. dist. 3.547771 adjlist NX
Z_20 x(8) Z_55 with generators [12,54]<>[8,16]:[16,2]<>[4,3]:[13,16]<>[7,23]:[17,37]<>[3,31]. Avg. dist. 3.547771 adjlist NX
Z_20 x(38) Z_55 with generators [7,18]<>[13,16]:[16,54]<>[4,31]:[3,35]<>[17,5]:[4,48]<>[16,2]. Avg. dist. 3.536852 (1,8,56,373,662) trans.: 3887 adjlist NX
Z_20 x(47) Z_55 with generators [8,43]<>[12,42]:[11,8]<>[9,34]:[19,17]<>[1,26]:[12,54]<>[8,16]. Avg. dist. 3.536852 (1,8,56,373,662) trans.: 3887 adjlist NX
Z_20 x(48) Z_55 with generators [11,5]<>[9,40]:[19,16]<>[1,2]:[12,3]<>[8,17]:[8,11]<>[12,44]. Avg. dist. 3.536852 (1,8,56,373,662) trans.: 3887 adjlist NX
Com_1640
Degree= 9, Diameter = 4; Order =1640; Moore bound=5266.
Cayley graph. Found as a semidirect product, 1640 nodes and 7380 (F.Comellas 2024):
- Z_40 x(22) Z_41, generators [23,14]<>[17,33]:[25,18]<>[15,13]:[27,35]<>[13,33]:[2,23]<>[38,8]:[20,3]<>[20,3]. Avg. dist.: 3.571080 (1,9,72,532,1026) transmission: 5853. adjlist NX
Z_40 x(24) Z_41, generators [25,28 ]<>[15,2 ]:[14,40 ]<>[26,33 ]:[29,11 ]<>[11,39 ]:[39,12 ]<>[1,40 ]:[20,35 ]<>[20,35 ]. Avg. dist.: 3.571080 (1,9,72,532,1026) transmission: 5853. adjlist NX
The two graphs are isomorphic.
--------------------
This SageMath script computes several properties of the graphs including symmetry group sizes. This is the online version .
--------------------
Former result, Order =1550
Communicated by Eyal Loz, Math Dep., Auckland Univ., New Zealand (July 2006)
Voltage graph Z_10 x(4) Z_155, B(1,4), voltages [(5, 0)|(7, 1)(4, 52)(6, 136)(1, 72)], avg. dist.: 3.555197
Z_m x(a) Z_n represents a semidirect product of cyclic groups [x,y][u,v]= [x + u mod m, y*a^u + v mod n].
Download the raw adjacency list of the graph.
Link to Eyal Loz's data (internet archive)
Found also as a semidirect product (F.Comellas 2023):
Z_10 x(4) Z_155 with generators [9,55]<>[1,90]:[6,126]<>[4,139]:[3,98]<>[7,13]:[6,142]<>[4,73]:[5,31]. Avg. dist. 3.555197 adjlist NX
Z_10 x(39) Z_155; generators [6,79]<>[45,6]:[9,1]<>[1,116]:[6,57]<>[4,113]:[3,130]<>[7,50]:[5,124]. Avg. dist. 3.555197 adjlist NX
Z_10 x(64) Z_155 with generators[9,132]<>[1,77]:[8,153]<>[2,132]:[7,19]<>[3,34]:[2,71]<>[8,114]:[5,0]. Avg. dist. 3.555197 adjlist NX
Com_2331
Degree= 10, Diameter = 4; Order =2331; Moore bound=8201.
Cayley graph. Found as a semidirect product, 2331 vertices, 11655 edges (F.Comellas 2024):
-
- Z_9 x(44) Z_259, generators [8,132]<>[1,81]:[2,171]<>[7,163]:[2,71]<>[7,101]:[4,236]<>[5,235]:[6,240]<>[3,124]. Avg. dist.: 3.580258 (1,10,90,768,1462) transmission: 8342. adjlist NX
-
- Z_9 x(81) Z_259, generators [5,102]<>[4,75]:[7,111]<>[2,37]:[2,94]<>[7,23]:[2,9]<>[7,27]:[6,10]<>[3,11]. Avg. dist.: 3.593133 (1,10,90,738,1492) transmission: 8372. adjlist NX
-
- Z_9 x(123) Z_259, generators [8,132]<>[1,81]:[2,171]<>[7,163]:[2,71]<>[7,101]:[4,236]<>[5,235]:[6,240]<>[3,124]. Avg. dist.: 3.599142 (1,10,90,724,1506) transmission: 8386. adjlist NX
-
- Z_9 x(256) Z_259, generators [5,235]<>[4,131]:[1,59]<>[8,106]:[2,102]<>[7,75]:[3,215]<>[6,219]:[8,194]<>[1,64]. Avg. dist.: 3.610300 (1,10,90,698,1532) transmission: 8412. adjlist NX
--------------------
This SageMath script computes several properties of the graphs including symmetry group sizes. This is the online version .
--------------------
Former result, Order = 2286
Communicated by Eyal Loz, Math Dep., Auckland Univ., New Zealand (July 2006)
Voltage graph Z_9 x(35) Z_254, B(0,5),
voltages [(2,253)(8,210)(5,38)(8,111)(4,37)],
Z_m x(a) Z_n represents a semidirect product of cyclic groups [x,y][u,v]= [x + u mod m, y*a^u + v mod n].
New record graphs in the degree-diameter problem. E. Loz, J. Širáň, Australas. J. Combin. 41 (2006), 63–80.
Link to Eyal Loz's data (internet archive)
Found also as a semidirect product (F.Comellas 2024):
Z_9 x(37) Z_254 with generators [3,179]<>[6,155]:[7,223]<>[2,21]:[7,152]<>[2,192]:[1,36]<>[8,102]:[1,209]<>[8,63] Avg. dist.: 3.591685 transmission: 8207 adjlist NX
Z_9 x(99) Z_254 with generators [1,34]<>[8,228]:[4,187]<>[5,193]:[3,205]<>[6,163]:[5,44]<>[4,40]:[8,199]<>[1 111] Avg. dist.: 3.589934 transmission: 8203 adjlist NX
Z_9 x(103) Z_254 with generators [5,136]<>[4,40]:[3,65]<>[6,157]:[5,114]<>[4,168]:[7,220]<>[2,26]:[7,230]<>[2,108] Avg. dist.: 3.601313 transmission: 8229 adjlist NX
Z_9 x(179) Z_254 with generators [4,249]<>[5,213]:[7,120]<>[2,132]:[3,117]<>[6,181]:[2,195]<>[7,235]:[2,227]<>[7,241] Avg. dist.: 3.597812 transmission: 8221 adjlist NX
Z_9 x(195) Z_254 with generators [7,19]<>[2,155]:[3,11]<>[6,45]:[2,23]<>[7,129]:[1,67]<>[8,225]:[8,150]<>[1,214] Avg. dist.: 3.585558 transmission: 8193 adjlist NX
Z_18 x(68) Z_127 with generators [5,72]<>[13,3]:[4,81]<>[14,39]:[15,59]<>[3,37]:[1,103]<>[17,90]:[5,119]<>[13,42] Avg. dist.: 3.597812 transmission: 8221 adjlist NX
Q7(T4)
Delta= 11, Diam= 4; N=3200; Moore bound=12222 ;
J. Gomez, M.A. Fiol. Dense Compound Graphs.Ars Combinatoria, 20-A (1985), pp. 211-237. link to the paper
Q′8*X8
Delta= 12, Diam= 4; N=4680; Moore bound= 17569;
Special product of bibartite graphs from C. Delorme.
C. Delorme. Grands graphes de degré et diamètre donnés.Eur. J. Comb. 6 (1985), pp. 291-302. (submitted 1982) link to the paper
Q9(T4)
Delta= 13, Diam= 4; N=6560; Moore bound= 24506;
J. Gomez, M.A. Fiol. Dense Compound Graphs.Ars Combinatoria, 20-A (1985), pp. 211-237. link to the paper
Q9(T5)
Delta= 14, Diam= 4; N=8200; Moore bound= 33321;
J. Gomez, M.A. Fiol. Dense Compound Graphs.Ars Combinatoria, 20-A (1985), pp. 211-237. link to the paper
Q11(T4)
Delta= 15, Diam= 4; N=11712; Moore bound = 44326 ;
J. Gomez, M.A. Fiol. Dense Compound Graphs.Ars Combinatoria, 20-A (1985), pp. 211-237. link to the paper
Q11(T5)
Delta= 16, Diam= 4; N=14640; Moore bound=57857 ;
J. Gomez, M.A. Fiol. Dense Compound Graphs.Ars Combinatoria, 20-A (1985), pp. 211-237. link to the paper

