Informe sobre estructuras de acceso

4. Esquemas lineales

El esquema de Shamir mostrado en la sección 2.1 puede verse como un caso particular de los denominados esquemas lineales. En estos esquemas, a cada participante P_i se le asocia un subespacio vectorial F_i de dimensión d_i dentro de un espacio vectorial E de dimensión d. Fijando bases públicas B_i de cada subespacio F_i, y un vector adicional v₀ para el secreto, la generación aleatoria de los fragmentos y del propio secreto se realiza del siguiente modo: Se toma un vector aleatorio r uniformemente distribuido en el espacio vectorial. El secreto generado es el producto escalar s = r ⋅ v₀, mientras que a cada participante P_i le son entregados los productos escalares de s con los vectores de la base B_i de su subespacio. Es decir, P_i recibe el fragmento s_i = {r ⋅ v_j∣v_j ∈ B_i}

Un conjunto A será autorizado si el vector v₀ puede expresarse como combinación lineal de los vectores de las bases de sus participantes. El algoritmo de reconstrucción consiste en recuperar el secreto mediante la misma combinación lineal calculada ahora con los fragmentos. Concretamente, si B_A = ⋃ _Pi∈AB_i, entonces

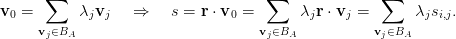
En el esquema de Shamir, el espacio vectorial utilizado es ℤ_p^t, que tiene dimensión igual al umbral t, y cada participante P_i está asociado a un único vector v_i = (1,x_i,x_i²,…,x _i^t−1). El vector del secreto es v ₀ = (1, 0,…, 0), y el vector aleatorio elegido es el vector de los coeficientes del polinomio r, r = (a₀,a₁,…,a_t−1), donde r(x) = a₀ + a₁x + …a_t−1x^t−1. La interpolación de Lagrange utilizada en el esquema de Shamir es equivalente al cálculo de los coeficientes λ_j del esquema lineal.

De modo similar a lo que ocurre con los esquemas de umbral con pesos, la eficiencia de los esquemas lineales decrece cuando las dimensiones d_i de los subespacios de los participantes aumenta. Sin embargo, existe una variedad considerable de estructuras de acceso diferentes de la de umbral que son realizables incluso si todos los d_i valen 1 (estructuras ideales), igualando la eficiencia del esquema de Shamir en lo que respecta al tamaño de la información secreta custodiada por los participantes.

Aunque los esquemas lineales permiten realizar cualquier estructura de acceso, la determinación de la asignación de subespacios a los participantes que asegure una realización eficiente de una estructura arbitraria es un problema combinatorio de difícil solución. Por ello, las construcciones usuales se restringen a familias concretas bien estudiadas, pero que aportan flexibilidad suficiente para la mayor parte de las aplicaciones.

Otra propiedad interesante de los esquemas lineales es que, al igual que el esquema de Shamir, éstos son aditivamente homomórficos. En efecto, si dos secretos han sido compartidos utilizando la misma asignación pública de vectores a los participantes, entonces sumar los vectores aleatorios es equivalente a sumar los secretos y los fragmentos de cada participante. Esto hace que gran número de protocolos criptográficos diseñados para funcionar con el esquema de umbral de Shamir puedan ser generalizados a cualquier esquema lineal, o como mínimo a cualquier esquema lineal ideal (es decir, donde d_i = 1).