En esta sección hacemos una descripción de las principales familias de estructuras de acceso con aplicabilidad práctica que generalizan el concepto de estructura de acceso de umbral.
Es posible componer varios esquemas de umbral para obtener estructuras de acceso más generales sin sacrificar excesivamente la eficiencia del esquema resultante. Los ejemplos más sencillos son las composiciones por conjunción y por disyunción.
Si tenemos dos estructuras de acceso Γ1 sobre 𝒫1 y Γ2 sobre 𝒫2, la conjunción de ambas es una estructura de acceso Γ1 ∧ Γ2 sobre la unión de los conjuntos de participantes 𝒫1 ∪𝒫2 en la que un conjunto A es autorizado si A ∩𝒫1 ∈ Γ1 y A∩𝒫2 ∈ Γ2, es decir, si los participantes de A forman un conjunto autorizado en ambas estructuras de partida. Claramente, la conjunción de dos estructuras es en general más restrictiva que las estructuras originales.
A partir de dos esquemas que realicen las estructuras Γ1 y Γ2 puede definirse
fácilmente (si se da alguna restricción técnica adicional) un esquema que realice la
conjunción de ambas. Para ello, un secreto s se reparte entre dos participantes
ficticios 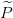 1,
1,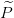 2 mediante un esquema de umbral (2, 2). Cada uno de
los dos fragmentos resultantes,
2 mediante un esquema de umbral (2, 2). Cada uno de
los dos fragmentos resultantes, 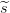 1,
1,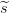 2, se reparte entre los participantes
reales utilizándolos como secretos en los esquemas que realizan Γ1 y Γ2,
respectivamente.
2, se reparte entre los participantes
reales utilizándolos como secretos en los esquemas que realizan Γ1 y Γ2,
respectivamente.
Observemos que la construcción anterior requiere que el conjunto de los posibles
secretos de los dos esquemas originales sean idénticos, para que podamos tomar
s = s1 + s2, de modo que s1 y s2 sean variables aleatorias uniformes e
independientes. Si las dos estructuras originales, Γ1, Γ2, son estructuras de
umbral (t1,n1) y (t2,n2) respectivamente, y se utilizan esquemas de Shamir para
realizarlas sobre el mismo cuerpo finito ℤp, entonces el esquema resultante para
la estructura Γ1 ∧ Γ2 sería el siguiente: El secreto s ∈ ℤp se descompone
aleatoriamente en suma de 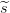 1,
1,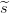 2 ∈ ℤp. Se construyen polinomios aleatorios r1(x)
y r2(x), de grado menor o igual que t1 y t2 respectivamente, tales que
r1(0) =
2 ∈ ℤp. Se construyen polinomios aleatorios r1(x)
y r2(x), de grado menor o igual que t1 y t2 respectivamente, tales que
r1(0) = 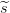 1 y r2(0) =
1 y r2(0) = 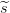 2. Finalmente, cada participante Pi ∈𝒫j recibe el
fragmento si,j = rj(xi,j), donde xi,j es el elemento público asociado a Pi
en el esquema de Shamir sobre el conjunto 𝒫j, con j = 1, 2. De este
modo, cada participante de la intersección 𝒫1 ∩𝒫2 recibirá dos fragmentos
independientes, mientras que los demás solamente recibirán uno de los dos
fragmentos.
2. Finalmente, cada participante Pi ∈𝒫j recibe el
fragmento si,j = rj(xi,j), donde xi,j es el elemento público asociado a Pi
en el esquema de Shamir sobre el conjunto 𝒫j, con j = 1, 2. De este
modo, cada participante de la intersección 𝒫1 ∩𝒫2 recibirá dos fragmentos
independientes, mientras que los demás solamente recibirán uno de los dos
fragmentos.
En el algoritmo de reconstrucción del secreto, se recuperan independientemente
los secretos parciales 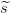 1 y
1 y 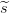 2 por medio de la interpolación de Lagrange, y
posteriormente se suman ambos para obtener s.
2 por medio de la interpolación de Lagrange, y
posteriormente se suman ambos para obtener s.
La construcción descrita puede generalizarse de modo natural a la conjunción de un número m > 2 de estructuras básicas. En el caso peor, un participante recibirá m fragmentos, uno por casa esquema básico en el que participa, que tendrá que custodiar en secreto hasta la reconstrucción. Por ello, para no degradar significativamente la eficiencia, m debe ser un número reducido.
En algunos casos, los conjuntos 𝒫1 y 𝒫2 son disjuntos, y la eficiencia de la conjunción es la misma que la de los esquemas originales. Un ejemplo de ello es un esquema en el que hay dos clases de participantes, y cada una de ellas tiene privilegios de reconstrucción diferentes, como el caso en el que el secreto puede ser recuperado siempre que un conjunto A contenga como mínimo t1 participantes de 𝒫1 y como mínimo t2 participantes de t2.
La disjunción de estructuras (y de esquemas) se define de manera análoga a la conjunción. La disjunción Γ1 ∨ Γ2 de dos estructuras de acceso Γ1 y Γ2 sobre 𝒫1 y 𝒫2 respectivamente, es una estructura de acceso definida sobre 𝒫1 ∪𝒫2 en la que un conjunto A es autorizado si o bien A ∩𝒫1 ∈ Γ1 o bien A ∩𝒫2 ∈ Γ2, es decir, si los participantes de A forman un conjunto autorizado en alguna de las dos estructuras de partida. La disyunción de dos estructuras es en general más amplia que las estructuras originales.
La construcción de un esquema para Γ1 ∨ Γ2 a partir de esquemas para cada una
de las estructuras originales es análoga a la de la conjunción salvo que ahora se
utiliza un esquema de umbral (1, 2) para combinarlos. Concretamente, se toma
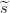 1 =
1 = 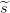 2 = s. Las consideraciones sobre la eficiencia del esquema resultante son
exactamente las mismas que en el caso anterior.
2 = s. Las consideraciones sobre la eficiencia del esquema resultante son
exactamente las mismas que en el caso anterior.
Existen construcciones aún más generales basadas en principios similares, en
las que m estructuras de acceso básicas, Γ1,…, Γm, se ensamblan en una
estructura más compleja por medio de otra estructura de referencia Γ0
con m participantes 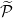 = {
= {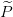 1,…,
1,…,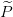 m}. Como antes, cada participante
ficticio
m}. Como antes, cada participante
ficticio 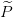 i se asocia a la estructura Γi sobre un conjunto de participantes
reales 𝒫i. El secreto s primero se reparte según un esquema que realice Γ0,
obteniendo fragmentos
i se asocia a la estructura Γi sobre un conjunto de participantes
reales 𝒫i. El secreto s primero se reparte según un esquema que realice Γ0,
obteniendo fragmentos 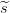 1,…,
1,…,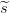 m asociados a los participantes ficticios.
Finalmente, esos fragmentos se toman como secretos a compartir entre los
usuarios reales, según las estructuras Γ1,…, Γm, respectivamente. En la
reconstrucción se procede, como en la conjunción y en la disyunción, en el orden
contrario: primero se reconstruyen algunos de los fragmentos de los
participantes ficticios, y luego a partir de ellos se reconstruye el secreto
real.
m asociados a los participantes ficticios.
Finalmente, esos fragmentos se toman como secretos a compartir entre los
usuarios reales, según las estructuras Γ1,…, Γm, respectivamente. En la
reconstrucción se procede, como en la conjunción y en la disyunción, en el orden
contrario: primero se reconstruyen algunos de los fragmentos de los
participantes ficticios, y luego a partir de ellos se reconstruye el secreto
real.
Las técnicas de conjunción y disyunción de estructuras permiten obtener construcciones generales (llamadas circuitales) válidas para cualquier estructura de acceso. Para ello, bastaría con expresar cualquier estructura de acceso como una composición conjunciones y disyunciones de estructuras de umbral. Un modo de hacerlo es asociar a cada estructura de acceso una fórmula booleana que de como resultado si un determinado conjunto de participantes es o no autorizado. Puede demostrarse que para cualquier estructura de acceso existe siempre una fórmula que utiliza únicamente los operadores lógicos de conjunción y de disyunción, pero no el de negación. En la construcción del esquema de compartir secretos, cada operación lógica en la fórmula corresponderá a una conjunción o una disyunción de estructuras de acceso.
Por ejemplo, si 𝒫 = {P1,P2,P3,P4} y los conjuntos autorizados son aquéllos que o bien contienen a P1 y a P2, o bien a P2 y a P3 o bien a P1, a P3 y a P4, entonces la estructura de acceso Γ puede asociarse a la fórmula booleana
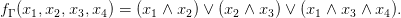
Sin embargo, esas construcciones generales son completamente imprácticas para la mayor parte de las estructuras de acceso posibles, por lo que conviene hacer un estudio de familias de estructuras particulares, suficientemente flexibles, que permitan construcciones eficientes de esquemas para compartir secretos que las realicen. En las siguientes secciones describiremos las familias conocidas más importantes.
En esta sección se describe la primera generalización natural de la estructura de acceso de umbral, en la que los participantes dejan de ser equivalentes para asociarles un peso distinto a cada uno de ellos. De este modo, la estructura permite diferenciar participantes con desigual relevancia en el procedimiento de reconstrucción del secreto. En particular, a cada participante Pi se le asigna un peso entero positivo wi, de modo que un conjunto de participantes se considera autorizado si la suma de los pesos de sus elemento supera cierto umbral t.
La estructura de acceso es fácilmente implementable mediante una sencilla modificación de un esquema de umbral (n′,t), donde n′ es ahora la suma de los pesos de todos los participantes, n′ = w1 + … + wn. Concretamente, a cada participante real Pi le son entregados wi fragmentos del esquema de umbral (n′,t). Dado que durante la reconstrucción del secreto, los participantes aportan sus fragmentos, un conjunto será autorizado si el número total de fragmentos que acumula (es decir, la suma de los pesos de sus participantes) alcanza el umbral t.
El esquema funciona como si cada participante Pi real jugase el papel de wi participantes virtuales diferentes en un esquema de umbral (n′,t).
Si bien la modificación anterior es muy simple, la eficiencia del esquema resultante se puede reducir considerablemente si los pesos adquieren un valor muy elevado. En particular, la cantidad de información secreta que recibirá el participante Pi será proporcional a su peso wi. Por ello, la aplicabilidad práctica del esquema se reduce a casos en los que la estructura de acceso deseada puede realizarse con valores muy reducidos de los pesos.
Una amplia familia de estructuras de acceso que contiene numerosos ejemplos de estructuras útiles en la práctica y que además son eficientemente implementables son las denominadas multipartitas o compartimentadas. En ellas, el conjunto de participantes está dividido en cierto número m de clases disjuntas, 𝒫1,…,𝒫m. Denotaremos por n1,…,nm el número de participantes en cada una de dichas clases. En una estructura multipartita un conjunto A es autorizado o no dependiendo únicamente del número de participantes de A en cada una de las clases. Es decir, serán los cardinales de A ∩𝒫1,…,A ∩𝒫m, que denotaremos por a1,…,am respectivamente, los que determinarán si A ∈ Γ. La definición anterior implica que en los esquemas multipartitos, los participantes pertenecientes a la misma clase son indistinguibles, sin importar la identidad particular de ninguno de ellos.
Este tipo de estructuras resulta muy natural cuando el secreto se reparte entre un colectivo numeroso y heterogéneo, pero divisible en un número reducido de clases o estamentos.
Por ejemplo, consideremos la siguiente estructura tripartita en la que un
conjunto A es autorizado si a1 ≥ t1 y a1 + a2 ≥ t2 o bien basta con que a3 ≥ t3.
Utilizando varios esquemas de Shamir ensamblados adecuadamente
puede construirse un esquema razonablemente eficiente que implemente
la estructura de acceso anterior. Concretamente, podemos combinar
esquemas de Shamir de umbral (t1,n1) en 𝒫1, de umbral (t2,n1 + n2) en
𝒫1 ∪𝒫2, y de umbral (t3,n3) en 𝒫3. Para repartir un secreto s ∈ ℤp,
lo dividimos aleatoriamente en la suma s = 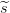 1 +
1 + 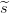 2, con
2, con 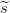 1,
1,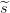 2 ∈ ℤp, y
utilizamos como secretos a compartir
2 ∈ ℤp, y
utilizamos como secretos a compartir 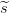 1,
1, 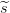 2 y s respectivamente en los tres
esquemas de Shamir mencionados. Claramente, los participantes de 𝒫1
recibirán dos fragmentos de Shamir, mientras que es resto recibirán un único
fragmento.
2 y s respectivamente en los tres
esquemas de Shamir mencionados. Claramente, los participantes de 𝒫1
recibirán dos fragmentos de Shamir, mientras que es resto recibirán un único
fragmento.
El ejemplo anterior podría utilizarse en situaciones como la de limitar el acceso a cierta información sensible en una empresa, de modo que se requiere la participación de como mínimo tres trabajadores de los que como mínimo uno tiene que ser responsable de proyecto, o bien basta con que sean dos auditores.
Una ventaja importante de este tipo de esquemas es que resulta sencillo incorporar nuevos participantes, simplemente generando nuevos fragmentos correspondientes a su clase, sin tener que cambiar ninguno de los fragmentos ya existentes. De todos modos, no todas las modificaciones naturales de la estructura pueden ser efectuadas de modo tan simple. Por ejemplo, si un participante cambia de una clase a otra, éste acumularía los privilegios de acceso de la nueva clase a la que pertenece a los que ya estaban en su poder. La revocación de privilegios de acceso requiere, en general, la renovación de todos los fragmentos y del secreto.
Las estructuras de acceso jerárquicas son casos particulares de estructuras multipartitas que, por su especial estructura, admiten esquemas de compartir secretos ideales. Existen dos tipos de estructuras jerárquicas: las conjuntivas y las disyuntivas.
En todas las estructuras jerárquicas consideramos las m clases disjuntas de
participantes, 𝒫1,…,𝒫m, con n1,…,nm participantes respectivamente, y
consideramos una secuencia entera de umbrales 0 < t1 <  < tm.
< tm.
En la estructura jerárquica disyuntiva un conjunto A es autorizado si existe algún número entero k, 1 ≤ k ≤ m, tal que a1 + … + ak ≥ tk, donde ai denota el número de participantes en A ∩𝒫i.
De modo análogo, en la estructura jerárquica conjuntiva A es autorizado si para todo k, 1 ≤ k ≤ m, se cumple que a1 + … + ak ≥ tk.