#bloc1.py
import networkx as nx
import pylab as p
# Creem un cert graph aleatori de 100 elements amb la probabilitat
# 0.015 que dos arestes estiguin connectades
G=nx.erdos_renyi_graph(100,0.015)
# Per mostrar-lo el podem dibuixar amb la instruccio
# Aquesta intenta optimitzar la seva posicio
nx.draw(G)
# Per dibuixar-lo de la manera mes rapida, podem dir-li que es aleatori
nx.draw_random(G)
# Anem a veure propietats del graf
# Aixo ens donara les seves components connexes:
nx.connected_components(G)
# i per tant, per saber el nombre de components connexes farem
len(nx.connected_components(G))
# o be
nx.number_connected_components(G)
# Podem també escriure les diferents components connexes en una llista de grafs:
H=nx.connected_component_subgraphs(G)
componentsconnexes=len(H)
# i dibuixar la component connexa més gran
nx.draw(H[0])
# Tambe podem estudiar el grau d'un node, p.ex. el node 29
nx.degree(G,29)
# El grau mitja
p.mean(nx.degree(G))
# L'histograma de graus
histograma= nx.degree_histogram(G)
# ara el dibuixem amb el pylab
p.hist(histograma)
# Per veure-ho encara millor, ho podem fer amb mes components
G=nx.erdos_renyi_graph(1000,0.01)
p.hist((nx.degree(G)))
# Anem a mirar ara la clusteritzacio del graf:
nx.clustering(G)
p.mean(nx.clustering(G))
# i l'histograma de connectivitats
p.hist(nx.clustering(G))
# Exercici: compareu els resultats quan preneu un graf regular:
L=nx.random_regular_graph(10,1000)
# que es un graph de 1000 elements i grau 10 de cadascun7 Simulació de Xarxes Complexes
En aquesta pràctica dibuixarem alguns dels grafs que hem vist a classe. El més senzill és un graf totalment aleatori, com el del Erdös-Renyi. Per iniciar, farem ipython -pylab. Usarem el paquet networkx
7.1 Alguns models de xarxes complexes
El model de Watts-Strogatz
Aquest model està implementat en el networkx:
# bloc2.py
import networkx as nx
import pylab as p
#Per crear un graf circular on cada graf es connecta amb
#2 veins per cada costat i la probabilitat de enllasos es 0
G=nx.watts_strogatz_graph(20,4,0.0)
nx.draw(G)
nx.draw_circular(G)
# Aquesta darrera instruccio es per mostrar millor la caracteristica circular del graf
# el model esdeve aleatori quan fem la probabilitat major a 1
G=nx.watts_strogatz_graph(20,4,0.1)
p.mean(nx.degree(G))
# L'histograma de graus
histograma= nx.degree_histogram(G)
# ara el dibuixem amb el pylab
p.hist(histograma)
# Per veure-ho encara millor, ho podem fer amb mes components
G=nx.watts_strogatz_graph(1000,4,0.01)
p.hist((nx.degree(G)))
# Anem a mirar ara la clusteritzacio del graf:
nx.clustering(G)
p.mean(nx.clustering(G))
# i l'histograma de connectivitats
p.hist(nx.clustering(G))
#Tambe podem calcular el cami mitja mes curt
#i com disminueix amb la probabilitat
nx.average_shortest_path_length(G)Exploreu el model de Barabasi-Albert amb la instrucció nx.barabasi_albert_graph? Feu-ne l’histograma.
7.2 Propietats estadístiques de percolació i similars
En un graf d’Erdös-Renyi podem intentar calcular la propietat de percolació a través de les següents instruccions
# bloc3.py
# Ara anem a calcular la criticalitat de la percolacio
import numpy as n
import networkx as nx
import pylab as p
probabilitats=n.arange(0,0.1,0.001)
componentsconnexes=n.arange(0,0.1,0.001)
r=0
for q in probabilitats:
G=nx.erdos_renyi_graph(200,q)
componentsconnexes[r]=nx.number_connected_components(G)
r=r+1
p.plot(probabilitats,componentsconnexes,'o--')
p.show()o, anat creant el graf a cada pas
# bloc3b.py
# Ara anem a calcular la criticalitat de la percolacio
# construint directament el graf
import numpy as n
import networkx as nx
import pylab as p
N=2000
ITERACIONS=10000
connexions=n.arange(0,ITERACIONS,1)
componentsconnexes=n.arange(0,ITERACIONS,1)
G=nx.random_regular_graph(0,N)
for q in connexions:
G.add_edge(p.randint(0,N),p.randint(0,N))
componentsconnexes[q]=nx.number_connected_components(G)
# Afegim un node aleatoriament
p.plot(connexions,componentsconnexes,'-')
p.show()que dóna la següent figura:
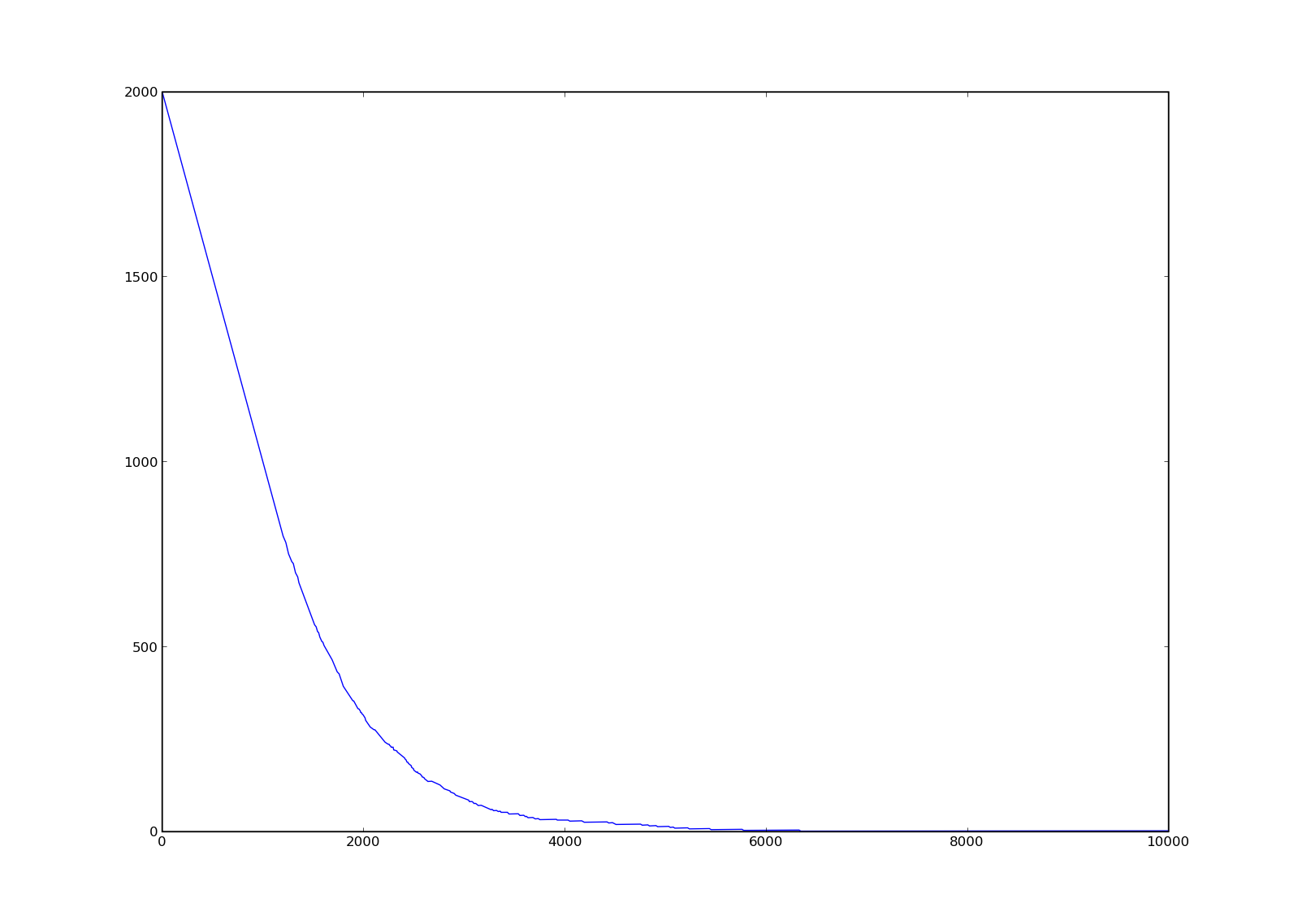
Per a xarxes tipus Watts-Strogatz podem estudiar com varia la connectivitat i el camí mitjà més curt en funció de la probabilitat de connexió:
# bloc4.py
# Ara anem a calcular com disminueix amb p
import numpy as n
import networkx as nx
import pylab as p
probabilitats=n.arange(0,1,0.01)
camimitja=n.arange(0,1,0.01)
clusteritzacio=n.arange(0,1,0.01)
r=0
for q in probabilitats:
G=nx.watts_strogatz_graph(200,4,q)
camimitja[r]=nx.average_shortest_path_length(G)
clusteritzacio[r]=p.mean(nx.clustering(G))
r=r+1
p.plot(probabilitats,camimitja,'o--')
p.plot(probabilitats,clusteritzacio,'o--')
p.show()Per aquest darrer és possible que hagueu d’actualitzar la versió del paquet NetworkX.