Largest Known (Degree, Diameter)-Graphs (Description)

Largest Known (Degree, Diameter)-Graphs

Diameter 2

Last modification June 22, 2025.

https://web.mat.upc.edu/francesc.comellas/old-files/delta-d/desc_g/desc_g2.html

raw adjacency list format: the first vertex of each row is adjacent to all the other vertices in that row.

implicit adjacency list format: each row corresponds to a vertex (row 1, vertex 0; row 2, vertex 1; and so on) and contains all vertices adjacent to it.

adjacency list NX NetworkX format. NetworkX format.

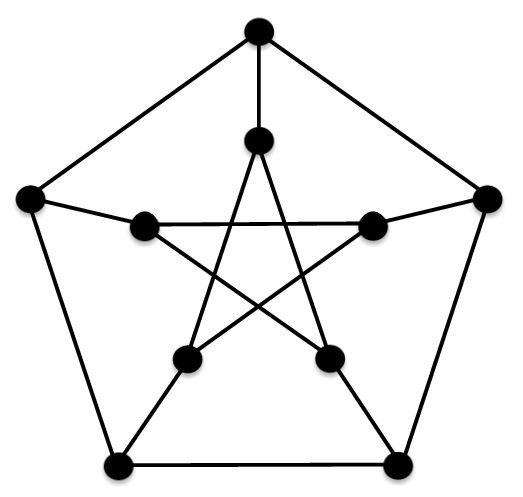
The Petersen Graph

Degree= 3, Diameter = 2; Order =10; Moore bound=10; Moore graph

Bibliography: Any book on Graph Theory, e.g. F. Comellas, J. Fàbrega, A. Sánchez, O. Serra. Matemática Discreta. Edicions UPC, Universitat Politécnica de Catalunya, 1994, 374 +ix pages, ISBN 84-7653-413-2 (Catalan); 2001, 344 pages. ISBN-13 978-8483014561 (Spanish)

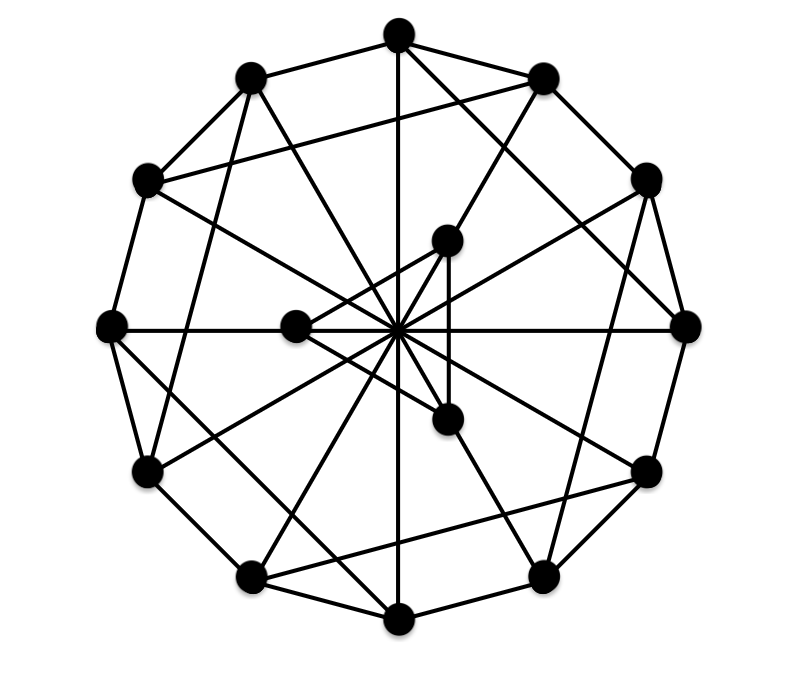
K3*C5

Delta= 4, Diam= 2; N=15; Moore bound=17; optimal.

See J.-C. Bermond, C. Delorme and G. Fahri. Large graphs with given degree and diameter II. J. Comb. Theory, Ser. B 36 (1984) 32-48. doi:10.1016/0095-8956(84)90012-1

Download the raw adjacency list or/and the NX adjacency list

This SageMath script computes several properties of K3xC5 including symmetry group size and the number of k-cycles (k=3..). This is the online version .

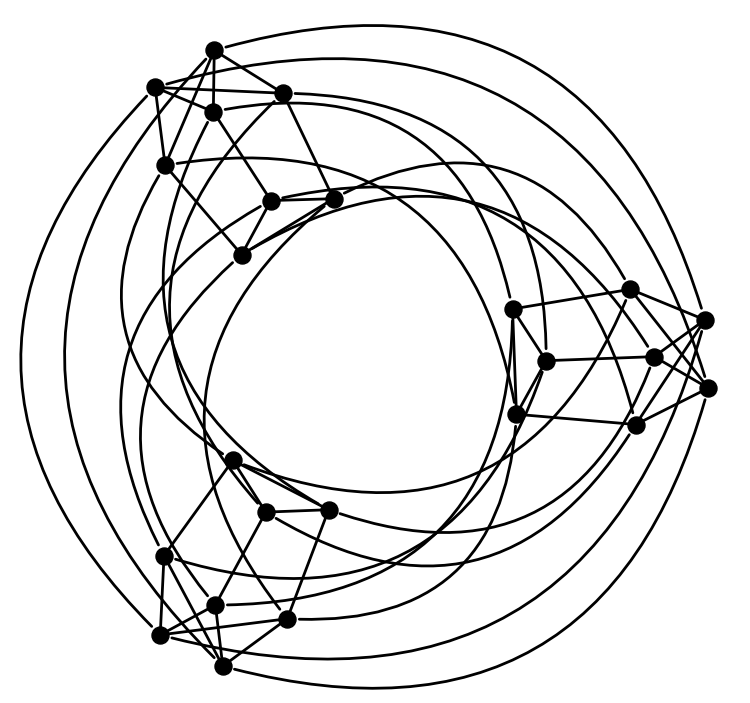
K3*X8

Delta= 5, Diam= 2; N=24; Moore bound=26; optimal.

See J.-C. Bermond, C. Delorme and G. Fahri. Large graphs with given degree and diameter III. Proc. Coll. Cambridge. 1981; Ann. Discrete Math. 13 (1982), 23-32. doi:10.1016/S0304-0208(08)73544-8

Download the implicit adjacency list or/and the NX adjacency list

This SageMath script computes several properties of K3xX8 including symmetry group size and the number of k-cycles (k=3..). This is the online version .

This Python program makes the figure and computes several properties of K3xX8. This is the online version .

K4*X8

Delta= 6, Diam= 2; N=32; Moore bound=37; optimal.

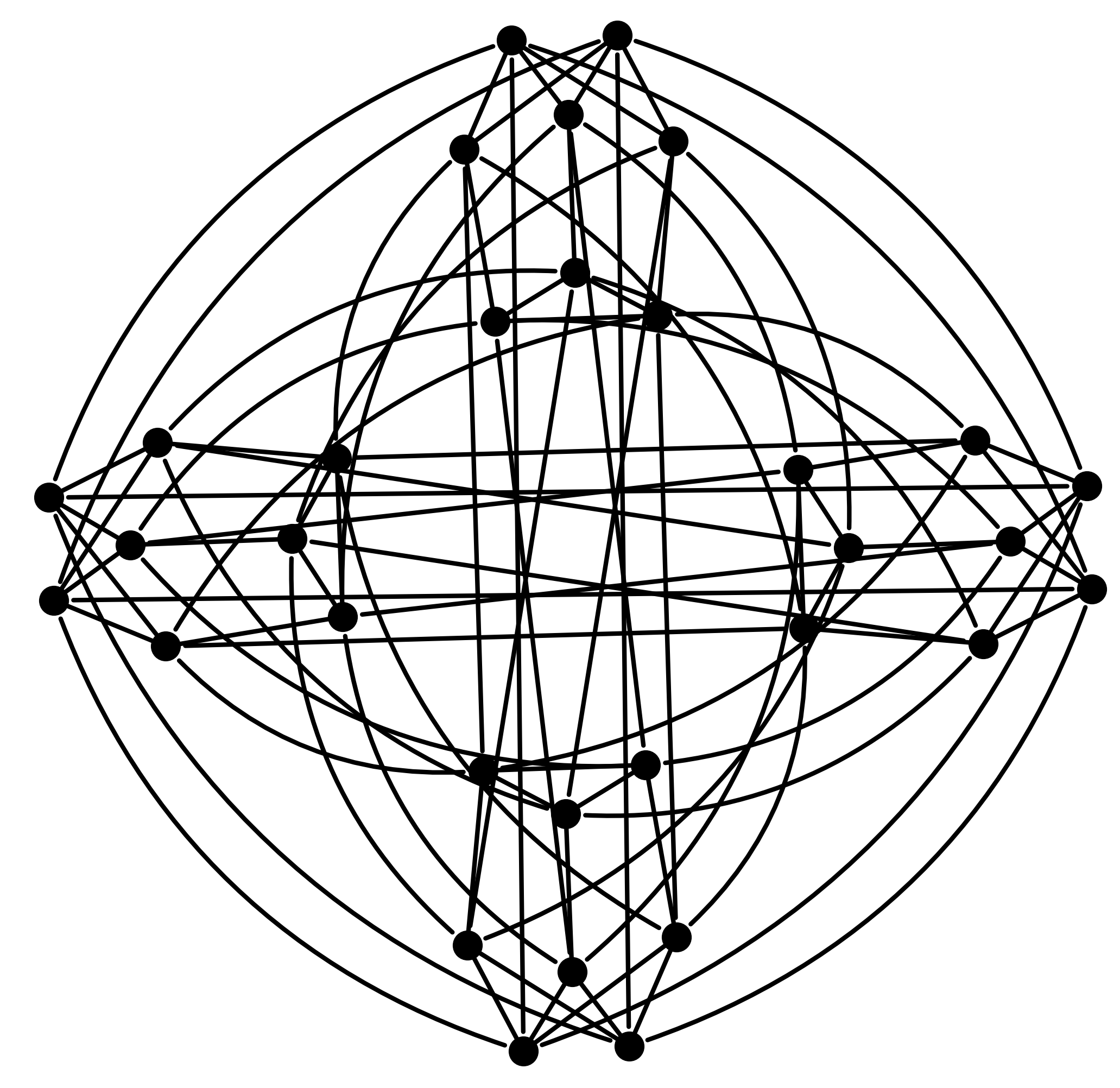K4*X8 was found by J.-C. Bermond, C. Delorme and G. Fahri. Large graphs with given degree and diameter III. Proc. Coll. Cambridge. 1981; Ann. Discrete Math. 13 (1982), 23-32. doi:10.1016/S0304-0208(08)73544-8

C. Delorme noticed the existence of another graph with 32 vertices, degree 6 and diameter 2: the Wegner graph. Here are his comments and the incidence list (1992).

Paul Hafner pointed out (July 1998) that the Wegner graph is isomorphic (with automorphism group of order 1920) to the graph described in:

Lutz Twele, Effiziente Implementierung des Todd-Coxeter Algorithmus im Hinblick auf Grad/Durchmesser-Optimierung von knotentransitiven Graphen, Diplomarbeit Universit"at Oldenburg, 1997 (the graph is also listed in Sampels' PhD thesis). Hafner provided a 'prettier' representation for this group and graph, all generators being involutions, < f > is the centre:

< a,b,c,d,e,f | a^2, b^2, c^2, d^2, e^2, f^2, (af)^2, (bf)^2, (cf)^2, (df)^2, (ef)^2, ababf, cbade, dbaec, ebacd, acacf, ecadb >

For some more info refer to: M.J.Dinneen, Group-Theoretic Methods for Designing Networks (http://www.cs.auckland.ac.nz/CDMTCS/researchreports/082nznews.pdf).

Guillermo Pineda commented (May 8, 2008) on the existence of a paper in LNCS v.4123 pp. 853-857 (2006) by Sergey G. Molodsov ("Largest Graphs of Diameter 2 and Maximum Degree 6" available at doi:10.1007/11889342_54 ) reporting his computer search which has generated all largest diameter 2 degree 6 graphs, resulting in 6 non isomorphic graphs with order 32 (one of them is K3xX8 and another the Wegner graph), and thus these graphs are optimal.

The following links go to the NetworkX adjacency lists and implicit adjacency lists of these graphs (extracted from the paper).

G1 (automorphism group of order 6) NX adj. list and impl. adj. list
G2 (automorphism group of order 2) NX adj. list and impl. adj. list
G3 (automorphism group of order 144) NX adj. list and impl. adj. list (K4*X8)
G4 (automorphism group of order 64) NX adj. list and impl. adj. list
G5 (automorphism group of order 48) NX adj. list and impl. adj. list
G6 (automorphism group of order 1920) NX adj. list and impl. adj. list (Wegner)

Note that the Wegner graph (G6) is a Cayley graph but is not edge-transitive. This SageMath script computes several properties of the six graphs including symmetry group sizes and the number of k-cycles (k=3..). This is the online version .

Hoffman-Singleton

Degree= 7, Diameter = 2; Order =50; Moore bound=50; Moore graph

Vertex set : \(V=(\alpha,i,j)\); \(\alpha \in \mathbb{Z}_2\); \(i,j \in \mathbb{Z}_5\).

Adjacencies : \((\alpha,i,j) \rightarrow (\alpha,i, j \pm (1+\alpha))\) and \((\bar{\alpha},l, j + (-1)^\alpha i l )\), \( ( l=0\ldots 4\); \(\bar{0}=1\), \(\bar{1}=0\).)

Details from Mathworld

Wikipedia entry

Download the implicit adjacency list

Download the NX adjacency list

This SageMath script computes several properties of the graph including symmetry group sizes and the number of k-cycles (k=3..). This is the online version .

P′₇

Degree= 8, Diameter = 2; Order =57; Moore bound=65

Quotient of the incidence graph of a of projective plane by a polarity.

C. Delorme and G. Farhi. Large graphs with given degree and diameter I. IEEE Trans. Comput, C-33:857–860, 1984. DOI: 10.1109/TC.1984.1676504

W.H. Haemers. Eigenvalue techniques in design and graph theory. Mathematical Centre Tracts 121, Mathematisch Zentrum, Amsterdam, 1980.

8 vertices have degree 7 and 49 degree 8

Download the implicit adjacency list of the graph (thanks to E. Canale).

This SageMath script computes several properties of the graph including symmetry group sizes and the number of k-cycles (k=3..). This is the online version .

P′₈d

Degree= 9, Diameter = 2; Order =74; Moore bound=82

Quotient of the incidence graph of a of projective plane by a polarity with duplication of some vertices.

C. Delorme and G. Farhi. Large graphs with given degree and diameter I. IEEE Trans. Comput, C-33:857–860, 1984. DOI: 10.1109/TC.1984.1676504

W.H. Haemers. Eigenvalue techniques in design and graph theory. Mathematical Centre Tracts 121, Mathematisch Zentrum, Amsterdam, 1980.

Graph with 74 vertices and 333 edges Degree Distribution: [0, 0, 0, 0, 0, 0, 0, 0, 74]

Download the implicit adjacency list of the graph (thanks to E. Canale).

This SageMath script computes several properties of the graph including symmetry group sizes and the number of k-cycles (k=3..). This is the online version .

P′₉

Degree= 10, Diameter = 2; Order =91; Moore bound=99

Quotient of the incidence graph of a of projective plane by a polarity.

C. Delorme and G. Farhi. Large graphs with given degree and diameter I. IEEE Trans. Comput, C-33:857–860, 1984. DOI: 10.1109/TC.1984.1676504

W.H. Haemers. Eigenvalue techniques in design and graph theory. Mathematical Centre Tracts 121, Mathematisch Zentrum, Amsterdam, 1980.

450 edges, 10 vertices have degree 9 and 81 degree 10.

Download the NX adjlist (NetworkX format) of the graph (thanks to E. Canale).

This SageMath script computes several properties of the graph including symmetry group sizes and the number of k-cycles (k=3..). This is the online version .

Exoo_104

Degree= 11, Diameter = 2; Order =104; Moore bound=122.

Communicated by G. Exoo (May 13, 2006). G.E. data

Download the implicit adjacency list of the graph.

Download the NX adjacency list of the graph.

This SageMath script computes several properties of the graph including symmetry group sizes and the number of k-cycles (k=3..). This is the online version .

P′₁₁

Degree= 12, Diameter = 2; Order =133; Moore bound=145.

Quotient of the incidence graph of a of projective plane by a polarity.

C. Delorme and G. Farhi. Large graphs with given degree and diameter I. IEEE Trans. Comput, C-33:857–860, 1984. DOI: 10.1109/TC.1984.1676504

W.H. Haemers. Eigenvalue techniques in design and graph theory. Mathematical Centre Tracts 121, Mathematisch Zentrum, Amsterdam, 1980.

792 edges, 12 vertices have degree 11 and 121 degree 12

Download the implicit adjacency list of the graph (thanks to E. Canale).

This SageMath script computes several properties of the graph including symmetry group sizes and the number of k-cycles (k=3..). This is the online version .

MKMS_162

Degree= 13, Diameter = 2; Order =162; Moore bound=170.

B.D. McKay, M. Miller, J. Siran; A note on large graphs of diameter two and given maximum degree. J. Comb. Theory Ser. B, 74 (1998) 110-118

--------------------

Download the raw adjacency list of the graph (thanks to B. McKay) and the NX adjlist

--------------------

This SageMath script computes several properties of the graphs including symmetry group sizes and the number of k-cycles (k=3,4,5). This is the online version .

P′₁₃

Degree= 14, Diameter = 2; Order =183; Moore bound=197.

Quotient of the incidence graph of a projective plane by a polarity.

C. Delorme and G. Farhi. Large graphs with given degree and diameter I. IEEE Trans. Comput, C-33:857–860, 1984. DOI: 10.1109/TC.1984.1676504

W.H. Haemers. Eigenvalue techniques in design and graph theory. Mathematical Centre Tracts 121, Mathematisch Zentrum, Amsterdam, 1980.

1274 edges, 14 vertices have degree 13 and 169 degree 14

Download the implicit adjacency list of the graph (thanks to E. Canale).

This SageMath script computes several properties of the graph including symmetry group sizes and the number of k-cycles (k=3..). This is the online version .

P′₁₃d

Degree= 15, Diameter = 2; Order =187; Moore bound= 226.

Quotient of the incidence graph of a projective plane by a polarity with some vertices added.

Description: Canale added 4 vertices to the graph with diameter 2 and max. degree 14 in a non-computer-generated way. The resulting graph has 1330 edges and 10 vertices have degree 13, 125 degree 14 and 52 degree 15 (average degree 14.224599). The average distance is 1.923524.

C. Delorme and G. Farhi. Large graphs with given degree and diameter I. IEEE Trans. Comput, C-33:857–860, 1984. DOI: 10.1109/TC.1984.1676504

W.H. Haemers. Eigenvalue techniques in design and graph theory. Mathematical Centre Tracts 121, Mathematisch Zentrum, Amsterdam, 1980.

Download the implicit adjacency list of the graph.

Download the adjacency list (NetworkX format).

This SageMath script computes several properties of the graph including symmetry group sizes and the number of k-cycles (k=3..). This is the online version .

Abas_200

Delta= 16, Diam= 2; N=200; Moore bound=257;
See "Large Networks of Diameter Two Based on Cayley Graphs" CSOC 2017: Cybernetics and Mathematics Applications in Intelligent Systems pp 225–233 DOI 10.1007/978-3-319-57264-2

Download a implicit adjacency list .

Download the adjacency list (NetworkX format).

This SageMath script computes several properties of the graph including symmetry group sizes and the number of k-cycles (k=3..). This is the online version .