Integrable Nonholonomic Systems
Such
systems had been subjects of my very first research projects
(concretely, the P. Appel problem on the "falling" disc and some
recent generalizations of the famous non-homogeneous Chaplygin
sphere). I still believe that such systems have a great future (of course,
in case of their fusion with mechatronics): this is one of few fields
where you can obtain new and nontrivial results without fully
understanding what you are doing ... Anyway, below are some examples.
Spherical hanging (support)
The classical Suslov problem
(motion of the body in space)
A special case of evolution of the
body frame in space between two opposite steady-state
rotations. (the animation created by A.Maciejewski)
This is one of the nontrivial
generalizations of the Chaplygin sphere problem:
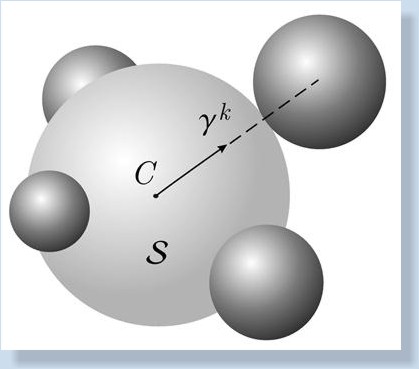
an axisymmettic ball S moves about its fixed center C,
the ball touches any number of dynamically symmetric spheres (also with
fixed centers) of any mass and radius, and there is no sliding at the
contact points.
The system describing the motion of
all the bodies is completely integrable.
It admits a reduction to a
non-Hamiltonian system on the group SO(3)
(the set of positions of the central ball), the generic invariant
manifolds of the reduced system are 2-dimensional tori.
(It also can be regarded as a
non-Hamiltonian generalization of the classical Euler top.) The
original reference is
Fedorov, Yu.
The motion of a rigid body in a
spherical support. (Russian)
Vestnik Moskov. Univ. Ser. I
Mat. Mekh. (1988), no.
5, 91--93 (PDF)
A detailed geometric description of
the problem can be found in section 4.2 of
A reduction of the reduced system to
quadratures (a very nontrivial one) was made in
This
problem describes the motion of a rigid body about a fixed point in
presence of a nonholonomic constraint. It is know that the evolution of
the angular velocity in the body frame is an asymptotic motion between
two opposite directions.
The motion of the body in space is also asymptotic, between two
steady-state rotations, whose axes, in general, are not opposite.
Recently a wide class of hypergeometric solutions was obtained, and the
angle between the axes of the limit steady-state rotations was
calculated in
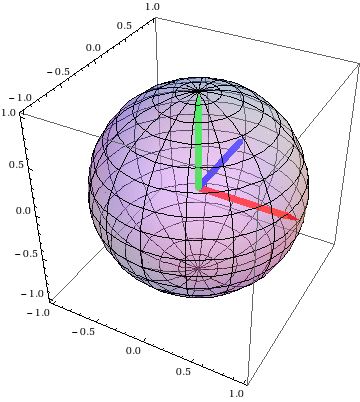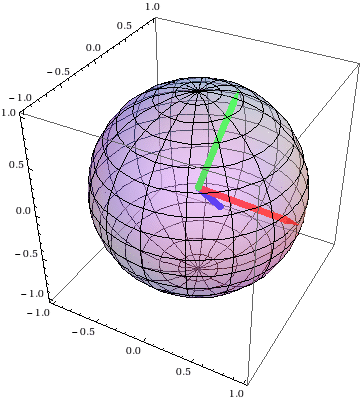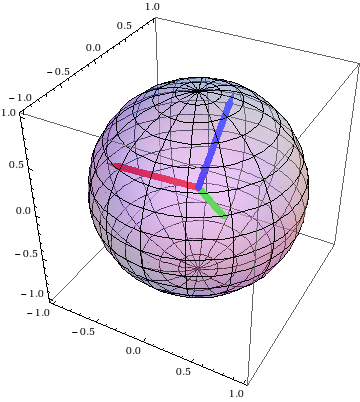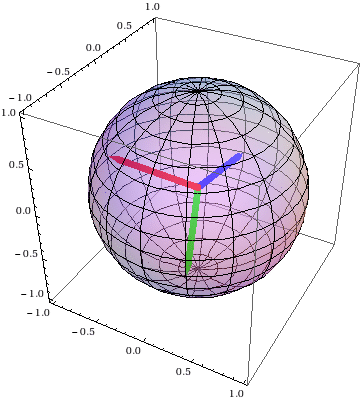
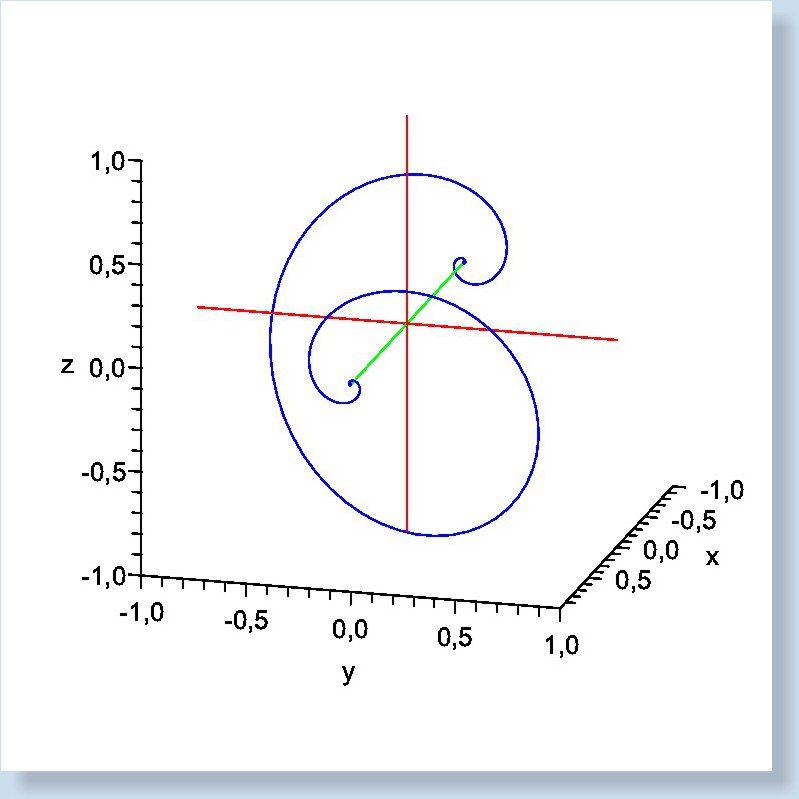
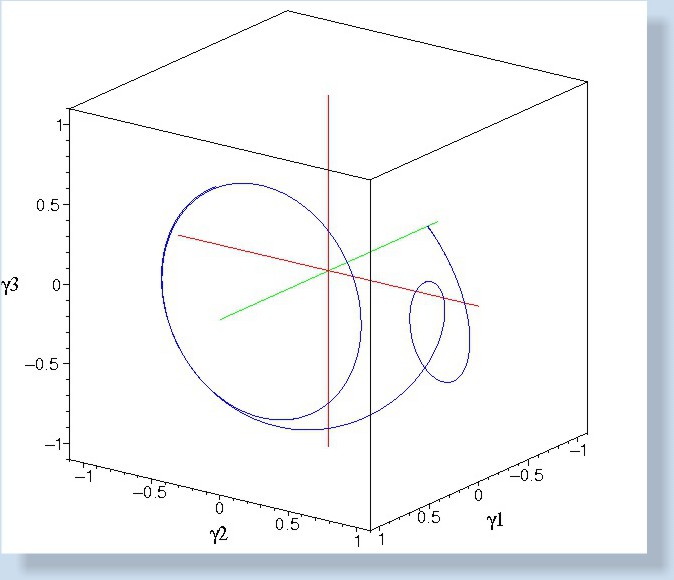
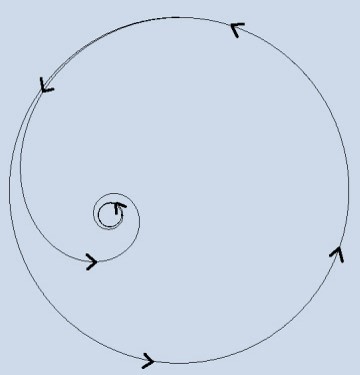
Spatial trajectories of a vector
fixed in the body:
←
the special case (left)
the general case (right) →
Hydrodynamic Chaplygin sleigh
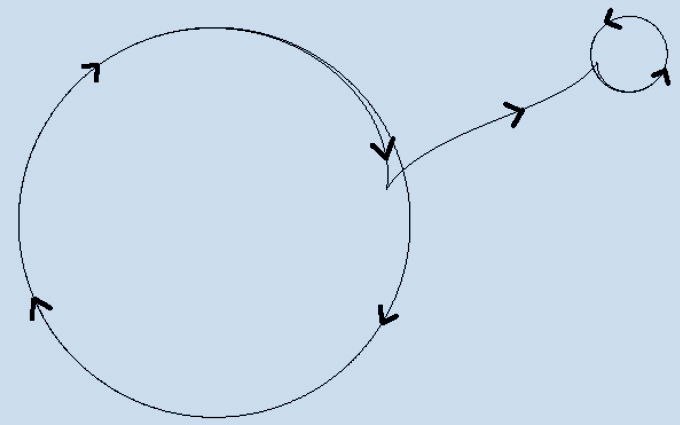
The classical Chaplygin sleigh is a
simple nonholonomic system with an asymptotic behavior: as time t
→±∞, the trajectory of the contact point (sleigh's blade) tends to
straight lines with a uniform motion.
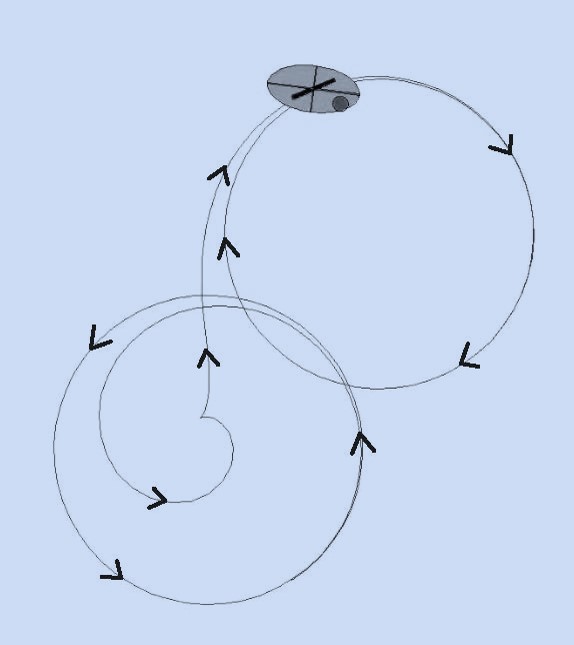
One of the nontrivial generalizations of this problem is the planar
motion of the sleigh in 2D ideal fluid (with or without circulation),
named Hydrodynamic Chaplygin sleigh.
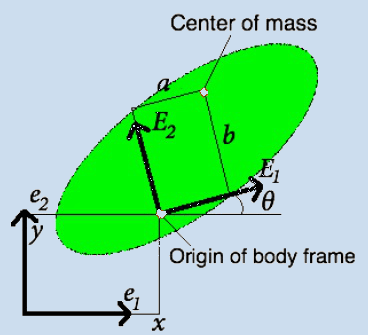
This system has new features: in general, when the tensor of adjoint
masses is disbalanced with respect to the axis of the blade and the
mass center (as depicted in the Fig. on the right),
the limit asymptotic trajectories of the contact point are
circumferences.
This system can be viewed as a first approximation to the
model of an underwater vehicle with a large fin.
In the following original papers various types of the dynamical
behavior of the sleigh are described and the explicit solutions were
presented.
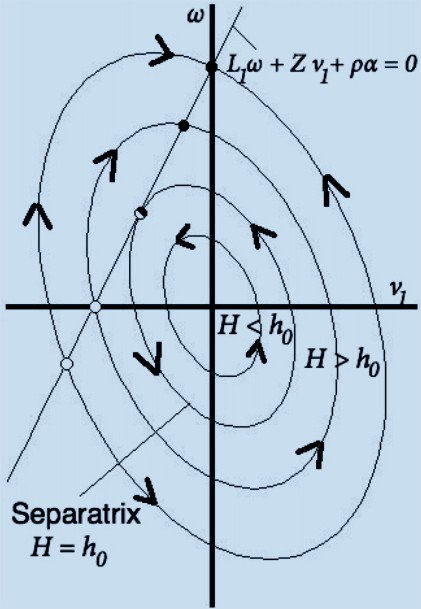
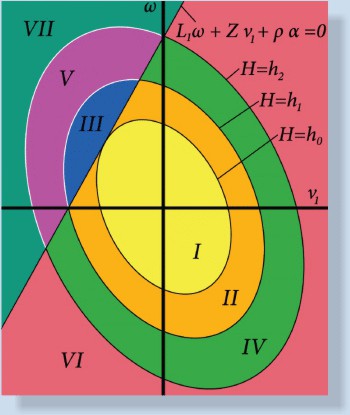
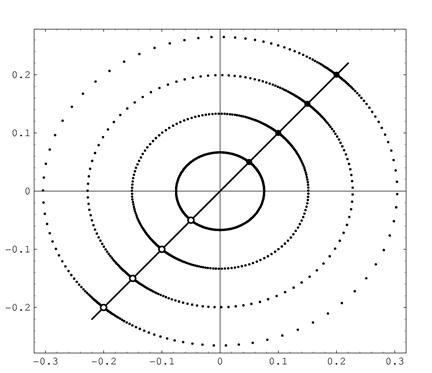
The phase portrait of the reduced
system on the plane (v1, ω),
v1= velocity along the blade axis;
ω = angular velocity of the
sleigh;
There is a line of (stable and unstable) fixed points, which correspond
to periodic circular motion of the sleigh. The trajectories are arcs of
ellipses or, near the origin, ellipses themselves. Special trajectories
divide the phase plane in 7 zones with different behaviour (as depicted
on the right). Some of the corresponding trajectories of the
sleigh blade in the 2D fluid are depicted below.
Discrete Nonholonomic LL Systems