Sympy in Quarto – Blog of Joaquim Puig

Sympy is a great piece of software for symbolic computations. Although there are many CAS, I particularly love this one because it is written purely in Python and you can document many of the computations that one currently does in teaching and research.

Although it is possible to use the Jupyter notebook as an engine, I prefer to use the {reticulate} package, which has now had a major update:

Sys.setenv(RETICULATE_PYTHON = "/usr/bin/python3")
library(reticulate)

In Quarto, moreover, this documentation can be written in a transparent way. Let us define a quasi-periodic Schrödinger matrix, where the symbols are written using unicode symbols (you could as well use emojis…).

Inserting Unicode Symbols

You can insert unicode symbols in GNU/Linux by pressing CRTL+SHIFT+U+<CODE>+ENTER where <CODE> is the code of your Unicode symbol. For instance, for the Greek alpha letter \(\alpha\), you could use CRTL+SHIFT+U+0+3+B+1+ENTER.

from sympy import *
var('a,b,θ,α', domain=RR)

(a, b, θ, α)

A=Matrix([[a-b*cos(2*pi*θ),-1],[1,0]])
A

Matrix([
[a - b*cos(2*pi*θ), -1],
[                1,  0]])

if you want the output the values in TeX you can use the latex output and define the cell output as asis

print('$$A='+latex(A)+'$$')

\[A=\left[\begin{matrix}a - b \cos{\left(2 \pi θ \right)} & -1\\1 & 0\end{matrix}\right]\]

Note - To include the full TeX output you need to enclose it into the equation environment you want to use. - You can also use pretty_print to output with a nice formatting and forget about LaTeX environments:

pretty_print(A)

[a - b*cos(2*pi*θ)  -1]
[                     ]
[        1          0 ]

We can substitute the values and simplify:

A0=(A.subs({b:0}));
A0.subs({a:2*cos(2*pi*α)});
λ1,λ2=A0.eigenvals()

and now print it (note the use of double \\ to get the right printing)

print('$$\\lambda_1='+latex(λ1)+'$$')

\[\lambda_1=\frac{a}{2} - \frac{\sqrt{\left(a - 2\right) \left(a + 2\right)}}{2}\]

and we can even insert the plots

plot(arg(λ1.subs({a:2*sin(pi*α)})),(α,0,1))

<sympy.plotting.plot.Plot object at 0x76d3e780d7f0>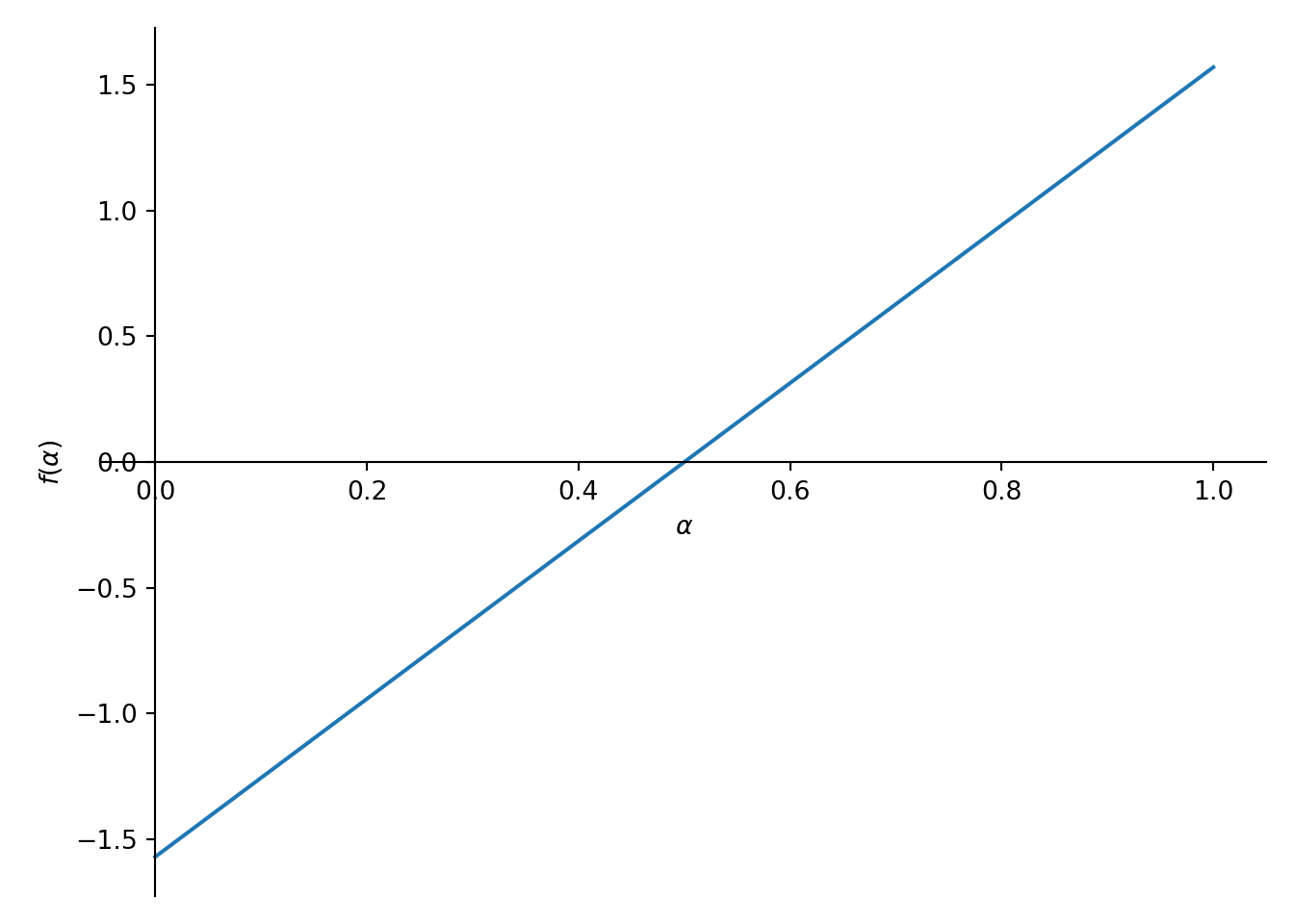

which means that the Schrödinger matrix when \(b=0\) above is conjugate to a rotation of angle \(\pi \alpha\) whenever \(a=2\sin{\pi \alpha}\) for \(\alpha \in [0,1]\).