En els darrers anys s'han considerat tècniques noves d'optimització amb ordinador que han donat bons resultats en el tractament de problemes combinatòris complexos. Aquests problemes consisteixen en trobar un mínim o màxim global d'una funció de cost definida en un conjunt d'estats (o de solucions possibles). D'entre aquestes tècniques destaquem les xarxes neuronals, la recuita simulada (simulated annealing) i els algorismes genètics. En aquest article es mostra la seva aplicabilitat al disseny de xarxes d'interconnexió i en concret al problema d'obtenir una xarxa d'interconnexió plana a partir d'una xarxa possiblement no plana. Es fa èmfasi, en particular, en la recuita simulada, mètode basat en l'analogia entre les configuracions possibles d'un problema d'optimització combinatòria i els estats d'un sistema físic del qual es busca l'estat d'energia mínima. La tècnica s'ha emprat per a determinar una funció de cost adequada als problemes d'aplanament. També, a la darrera secció, s'ha comparat la seva efectivitat en relació als algorismes genètics.

Figura 1. L'algorisme de recuita simulada.
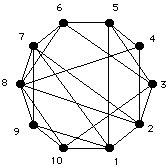
Figura 2. El graf de 22 branques estudiat per Jayakumar et al.
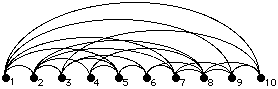
Figura 3. Representació en fila del graf de Jayakumar.
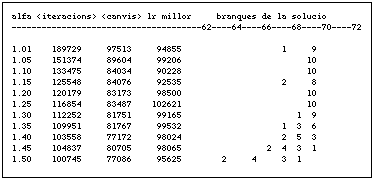
Taula 1. Estudi de la convergència de l'algorisme per a diferents valors d'$\alpha$. Graf aleatori d'ordre 30 i 72 branques.
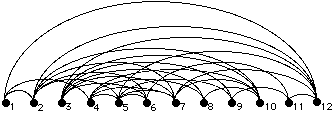
Figura 4. Graf aleatori de 12 vèrtexs i 28 branques.

Figura 5. Graf pla obtingut per recuita simulada del graf de la figura anterior.
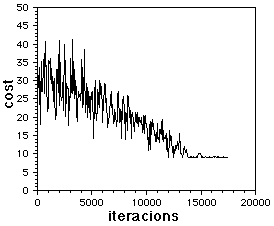
Figura 6. Variació del cost del graf a cada iteracio. Graf aleatori d'ordre 12 i 28 branques ($\alpha=1.13$)
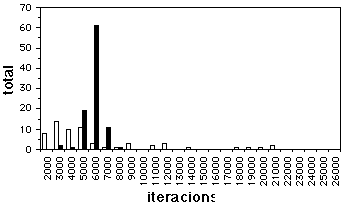
Figura 7. Graf de Jayakumar. Comparació entre la recuita simulada (negre) i l'algorisme genètic (blanc)
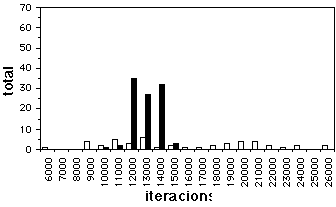
Figura 8. Graf aleatori de 12 vèrtexs i 28 branques. Comparació entre la recuita simulada (negre) i l'algorisme genètic (blanc)