Largest Known (Degree, Diameter)-Graphs

Diameter 5

Last modification: June 22, 2025.
https://web.mat.upc.edu/francesc.comellas/old-files/delta-d/desc_g/desc_g5.html
row adjacency list format: the first vertex of each row is adjacent to all the other vertices in that row.
implicit adjacency list format: each row corresponds to a vertex (row 1, vertex 0; row 2, vertex 1; and so on) and contains all vertices adjacent to it.
adjacency list NX NetworkX format. NetworkX format.
vC, AFY
Delta= 3, Diam= 5; N=70; Moore bound=94;
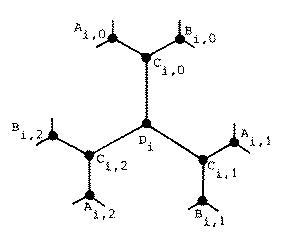Graph obtained by connecting seven clusters like the one shown in the figure with edges as

\(\large A_{i,j } \leftrightsquigarrow B_{i \pm 2^j, j \pm 1}, \;\; i = 0..6 \;\; and \;\; j = 0..2 \)

Download the adjacency list of the graph in NetworkX format (vertices notation as in AlFiYe86).
Download the adjacency list of the graph in NetworkX format (vertices labeled 0,2,...69).

The same graph can be constructed (Francesc Comellas, 2024) following the procedure from Jianxiang Cheng for the (3,8)=360 graph:
The graph is derived, in this case, from the Coxeter symmetric graph on 28 vertices (diameter 4, girth 7) by a complete pairing of its edges.
Let Cox be the Coxeter graph and ~ the pairing relation on its edges (0,1)->(19,20).
The graph is constructed as follows: The vertex set of the new graph H is V(Cox)∪E(Cox). If v∈V(Cox), u∈V(Cox), then they are not connected in H. If v∈V(Cox), u∈E(Cox), then they are connected in H iff v∈u in G. If v∈E(Cox), u∈E(Cox), then they are connected in H iff v~u by the pairing relation.
Download the adjacency list of the graph in NetworkX format (vertices labeled 0,2,...69).
Download a SageMath program to generate the graph in sparse6 format. This SGM program online
Download a Python program to check the graph. Can be easily adapted to check graphs in all other formats on this website. This Python program online
This SageMath script computes several properties of the graphs including symmetry group sizes and the number of k-cycles (k=3..10). This is the online version .
H′3
Delta= 4, Diam= 5; N=364; Moore bound=485;
Quotient by a polarity of the incidence graph of the regular bipartite generalized hexagon H3′.
Obtained by C. Delorme (1981) - see pag.11 of J-C. Bermond, B. Bollobas. The Diameter of Graphs: a survey. Congr. Numer. 32 (1981) pp. 3-27, Boca Raton, US.
C. Delorme, G. Farhi. Large graphs with given degree and diameter. IEEE Trans, Comput. c-33 (1984), pp. 857-860.
C. Delorme. Grands graphes de degré et diamètre donnés. European J. Combin. 6 (1985), pp. 291-302.
Download the adjacency list of the graph in NetworkX format (thanks to Vlad Pelekhaty).
This SageMath script, computes several of its properties. This is the online version. .
Loz_624
Delta= 5, Diam= 5; N=624; Moore bound=1706;
Download the raw adjacency list of the graph.
Communicated by Eyal Loz, Math Dep., Auckland Univ., New Zealand (July 2006)
Link to Eyal Loz's data
E. Loz, J. Širáň. New record graphs in the degree-diameter problem. Australas. J. Combin. 41 (2008), 63–80.
Loz_1404
Degree= 6, Diameter = 5; Order =1404; Moore bound=4687
Communicated by Eyal Loz, Math Dep., Auckland Univ., New Zealand (July 2006)
Download the raw adjacency list of the graph.
Link to Eyal Loz's data
E. Loz, J. Širáň. New record graphs in the degree-diameter problem. Australas. J. Combin. 41 (2008), 63–80.
DH_2756
Degree= 7, Diameter = 5; Order =2756; Moore bound=10886.
Obtained as a Cayley graph for semidirect product of Zm with Zn
Z_52 x(2)Z_53 with generators [25,45]<>[27,37] (order 52); [30,23]<>[22,18] (order 26); [40,39]<>[12,51] (order 13); [26,0] (order 2) . Avg.dist.: 4.332123 transm.: 11935 adjlist NX
Dinneen,M.J. & Hafner,P.; New results for the degree/diameter problem. Networks, 24 (1994) 359-367.
Other instances (F.Comellas 2024):
Z_52 x(8)Z_53 with generators [25,45]<>[27,37];[30,23]<>[22,18]; [40,39]<>[12,51];[26,0]. Avg. dist. 4.332123 transm.: 11935 adjlist NX
Z_52 x(8)Z_53 with generators [47,30]<>[5,4]; [42,51]<>[10,21]; [7,38]<>[45,50]; [26,8]. Avg. dist. 4.332123 transm.: 11935 adjlist NX
Z_52 x(12)Z_53 with generators [36,26]<>[16,50]; [38,32]<>[14,19]; [45,22]<>[7,17]; [26,22]. Avg. dist. 4.341198 transm.: 11960 adjlist NX
Z_52 x(18)Z_53 with generators [23,8]<>[29,16]; [38,41]<>[19,39]; [16,39]<>[36,51]; [26,13]. Avg. dist.4.332123 transm.: 11935 adjlist NX
Com_5115
Degree= 8, Diameter = 5; Order =5115; Moore bound=22409
Cayley graph. Found as a semidirect product, 5115 vertices, 20460 edges (F.Comellas 2024):
  1. Z_15 x(20) Z_341, generators [2,107]<>[13,108]:[12,80]<>[3,57]:[11,236]<>[4,294]:[5,13]<>[10,152]. Avg. dist.:4.393821 (1,8,56,384,2132,2534) transm.: 22470. adjlist NX
  2. Z_15 x(49) Z_341, generators [1,56]<>[14,145]:[4,220]<>[11,319]:[13,75]<>[2,134]:[8,17]<>[7,312]. Avg. dist.: 4.382088 (1,8,56,392,2176,2482) transmission: 22410. adjlist NX
  3. Z_15 x(69) Z_341, generators [7,100]<>[8,116]:[11,31]<>[4,217]:[14,182]<>[1,59]:[12,327]<>[3,59]. Avg. dist.: 4.380915 (1,8,56,390,2186,2474) ) transmission: 22404. adjlist NX
  4. Z_15 x(71) Z_341, generators [41,113]<>[1,161]:[10,181]<>[5,94]:[11,57]<>[4,224]:[2,176]<>[13,242]. Avg. dist.: 4.383262 (1,8,56,386,2182,2482) transm.: 22416 . adjlist NX
  5. Z_15 x(113) Z_341, generators [4,218]<>[11,303]:[11,113]<>[4,285]:[8,321]<>[7,81]:[1,166]<>[14,249]. Avg. dist.: 4.380524 (1,8,56,392,2184,2474) transm.: 22402. adjlist NX
  6. Z_15 x(152) Z_341, generators [2,90]<>[13,269]:[4,162]<>[11,60]:[9,104]<>[6,10]:[8,102]<>[7,153]. Avg. dist.: 4.400469 (1,8,56,384,2098,2568) transm.: 22504 . adjlist NX
  7. Z_15 x(169) Z_341, generators [3,92]<>[12,2]:[4,40]<>[11,291]:[1,99]<>[14,66]:[8,102]<>[7,139] . Avg. dist.: 4.400469 (1,8,56,384,2098,3568) transmission: 22504. adjlist NX
  8. Z_15 x(196) Z_341, generators [7,2]<>[8,313]:[14,38]<>[1,54]:[5,202]<>[10,106]:[7,116]<>[8,81]. Avg. dist.: 4.382088 (1,8,56,392,2176,2482) transm.: 22410. adjlist NX
  9. Z_15 x(235) Z_341, generators [2,239]<>[13,335]:[3,191]<>[12,332]:[5,42]<>[10,255]:[3,19]<>[12,158]. Avg. dist.: 4.380524 (1,8,56,388,2192,2470) transmission: 22402. adjlist NX
  10. Z_15 x(236) Z_341, generators [9.154]<>[6,33]:[2,1371]<>[13,35]:[1,140]<>[14,115]:[7,80]<>[8,24]. Avg. dist.: 4.400469 (1,8,56,384,2098,2568) transm.: 22504. adjlist NX
  11. Z_15 x(267) Z_341, generators [13,277]<>[2,257]:[1,290]<>[14,50]:[4.21]<>[11,69]:[10,258]<>[5,105]. Avg. dist.: 4.378178 (1,8,56,392,2196,2462) transm.: 22390. adjlist NX
  12. Z_15 x(267) Z_341, generators [14,162]<>[1,53]:[6,175]<>[9,114]:[8,18]<>[7,91]:[9,340]<>[6,157]. Avg. dist.:4.390301 (1,8,56,388,2142,2520) transm.: 22452. adjlist NX
  13. Z_15 x(289) Z_341, generators [6,280]<>[9,46]:[1,18]<>[14,302]:[2,49]<>[13,272]:[5,340]<>[10,67]. Avg. dist.: 4.393821 (1,8,56,384,2132,2534) transm.: 22470. adjlist NX
  14. Z_15 x(317) Z_341, generators [6,152]<>[9,241]:[5,136]<>[10,227]:[9,135]<>[6,204]:[11,33]<>[4,220]. Avg. dist.: 4.380524 (1,8,56,388,2192,2470) transmission: 22402. adjlist NX
  15. Z_15 x(324) Z_341, generators [14,24]<>[1,67]:[8,7]<>[1,177]:[6,118]<>[9,148]:[13,168]<>[2,211]. Avg. dist.: 4.409855 (1,8,56,384,2050,2626) transmission: 22552. adjlist NX
Graphs 1 and 13, with transmission 22470, are isomorphic. Distance distribution: (8, 56, 384, 2132, 2534). Cycle distribution: (0, 0, 1023, 5115, 51150, 271095, ..)
Graphs 2 and 8, boh with transmission 22410 and distance distribution (8, 56, 392, 2176, 2482)are not isomorphic and they have a different cycle distribution: (0, 0, 0, 0, 51150, 312015, ...) vs (0, 0, 0, 0, 71610, 281325, ..).
Graphs 6, 7 and 10 with transmission 22504, are isomorphic. Distance distributions,(1,8,56,384,2098,2568). Cycle distribution: (0, 0, 1023, 5115, 51150, 296670, ..)
Graphs 5, 9, and 14, all have transmission 22402. Graphs 9 and 14 are isomorphic with distance distribution (8, 56, 388, 2192, 2470), but are not isomorphic to Graph 5 wich has distance distribution (8, 56, 392, 2184, 2474).

Former result, Order = 5060. Communicated by Eyal Loz, Math Dep., Auckland Univ., New Zealand (July 2006)
Voltage graph Z_44 x(2) Z_115, B(0,4), voltages [(25,14)(2,21)(7,25)(32,29)], avg. dist.: 4.377743
Z_m x(a) Z_n represents a semidirect product of cyclic groups [x,y][u,v]= [x + u mod m, y*a^u + v mod n].
(raw adjacency list from Loz ) ::: Link to Eyal Loz's original data. --- adjlist NX version.
E. Loz, J. Širáň. New record graphs in the degree-diameter problem. Australas. J. Combin. 41 (2008), 63–80.
Found also as a semidirect product, some instances have a lower average distance (F.Comellas 2024):
Z_44 x(2) Z_115 with generators [37,104]<>[7,28]:[2,95]<>[42,5]:[25,66]<>[19,32]:12,58]<>[32,17]. Avg.dist.: 4.377743 transm.: 22147 adjlist NX
Z_44 x(32) Z_115 with generators [28,34]<>[16,96]:[25,10]<>[19,100]:[42,31]<>[2,111]:[27,51]<>[17,8]. Avg.dist.: 4.374580 transm.: 22131 adjlist NX
Rod_8268
Degree= 9, Diameter = 5; Order =8268; Moore bound=42130.
Communicated by Alexis Rodriguez, Fac. Ing., Univ. Republica, Montevideo (June 2012)
"Graph with 8268 vertices, 37206 edges, diameter 5, avg. dist.4.415991 and maximum degree 9. Obtained with the group Z_52 x(2) Z_159, quotient B(1,4), voltages: (14,41), (47,112), (37,82), (10,113), (26,147)"
A. Rodríguez de los Santos (2013.). Búsquedas masivas de grafos de gran orden con grado y diámetro acotados. Tesis de maestría. Universidad de la República (Uruguay). Facultad de Ingeniería. (implicit adjacency list from Alexis) --- adjlist NX version.
Found also as a semidirect product. All instances have a lower average distance (F.Comellas 2024):
Z_52 x(41) Z_159 with generators [11,77]<>[41,65]; [29,134]<>[23,125]; [24,103]<>[28,98]; [38,32]<>[14,19]; [26,105] . Avg.dist.: 4.408975 transm.: 36449 adjlist NX
Z_52 x(50) Z_159 with generators [33,82]<>[19,85]; [47,78]<>[5,33]; [6,80]<>[46,157]; [30,113]<>[22,40]; [26,275] . Avg.dist.:4.400992 transm.: 36383 adjlist NX
Z_52 x(71) Z_159 with generators [16,142]<>[36,149]; [21,31]<>[31,1]; [9,90]<>[43,108]; [3,73]<>[49,43]; [26,108] . Avg.dist.: 4.398452 transm.: 36362 adjlist NX
Com_13203
Degree= 10, Diameter = 5; Order = 13203
Cayley graph. Found as a semidirect product, 13203 vertices, 66015 edges (F.Comellas 2024):
  1. Z_81 x(22) Z_163, generators [49,70]<>[32,131]:[64,134]<>[17,63]:[78,95]<>[3,18]:[45,156]<>[36,80]:[14,90]<>[67.63]. Avg. dist. 4.426299 (1,10,90,804,5656,6642) transm.: 58274 adjlist NX
  2. Z_81 x(24) Z_163, generators [14,82]<>[67,161]:[73,41]<>[8,3]:[59,115]<>[22,19]:[5,110]<>[76,69]:[69,66]<>[12,160]. Avg. dist. 4.433419 (1,10,90,802,5566,6734) transm.: 58530 adjlist NX
  3. Z_81 x(34) Z_163, generators [69,53]<>[12,138]:[22,108]<>[59,161]:[18,157]<>[63,25]:[31,0]<>[50,0]:[66,44]<>[15,47]. Avg. dist. 4.426905 (1,10,90,808,5640,6654) transm.: 58444 adjlist NX
  4. Z_81 x(36) Z_163, generators [73,95]<>[8,124]:[71,122]<>[10,121]:[47,140]<>[34,27]:[57,162]<>[24,133]:[7,114]<>[74,84]. Avg. dist. avg. dist.: 4.436146 (1,10,90,810,5614,6778) transm.: 58566 adjlist NX
  5. Z_81 x(51) Z_163, generators [67,56]<>[14,3]:[43,106]<>[38,14]:[16,139]<>[65,64]:[72,134]<>[9,124]:[30,117]<>[51,119]. Avg. dist. avg. dist.:4.432056 (1,10,90,796,5596,6710) transm.: 58512 adjlist NX

Previous results, Order = 13149 F.Comellas. download the adjacency list (NX format)

Former result, Order = 13140. Communicated by Eyal Loz, Math Dep., Auckland Univ., New Zealand (July 2006)
Voltage graph Z_36 x(18) Z_365, B(0,5), voltages [(6,263)(5,2)(20,201)(29,325)(14,169], avg. dist.: 4.434051
Z_m x(a) Z_n represents a semidirect product of cyclic groups [x,y][u,v]= [x + u mod m, y*a^u + v mod n].
(raw adjacencies from Loz ) ::: Link to Eyal Loz's original data. --- adjlist NX version.
E. Loz, J. Širáň. New record graphs in the degree-diameter problem. Australas. J. Combin. 41 (2008), 63–80.
Found also as a semidirect product, some instances have a lower average distance (F.Comellas 2024):
Z_36 x(2) Z_365 with generators [19,111]<>[17,273]; [25,222]<>[11,134]; [3,157]<>[33,26]; [29,323]<>[7,266]; [16,254]<>[20,6] . Avg.dist.: 4.431311 transm.: 58223 adjlist NX
Z_36 x(32) Z_365 with generators [22,241]<>[14,359]; [19,335]<>[17,115]; [2,356]<>[34,41]; [14,278]<>[22,348]; [4,294]<>[32,36]. Avg. dist. 4.425527 transmission 58147 adjlist NX
Z_36 x(142) Z_365 with generators [31,300]<>[5,235]; [18,12]<>[18,207]; [25,355]<>[11,205]; [1,194]<>[35,158]; :[35,286]<>[1,268] . Avg. dist. 4.431007 transm.: 58219 adjlist NX
Z_36 x(148) Z_365 with generators [1,59]<>[35,7]; [20,331]<>[16,264]; [21,260]<>[15,150]; [11,193]<>[25,116]; [32,264]<>[4, 156]. Avg. dist.4.433899 transm.: 58257 adjlist NX

Com_19620
Degree= 11, Diameter =5; Order = 19620; Moore bound = 122221.
Cayley graph. Found as a semidirect product, 19620 nodes and 107910 edges (F.Comellas 2024):
  1. Z_36 x(241) Z_545 generators [4,19 ]<>[32,381 ]:[26,165 ]<>[10,430 ]:[19,414 ]<>[17,236 ]:[15,426 ]<>[21,519 ]:[35,524 ]<>[1,156 ]:[18,15 ]<>[18,15 ]. Avg. dist.: 4.445945 (1,11,110,1088,8320,10090) transm.: 87225 adjlist NX
    3. Z_36 x(434) Z_545 generators [22,21 ]<>[14,49 ]:[30,484 ]<>[6,416 ]:[22,513 ]<>[14,107 ]:[33,116 ]<>[3,56 ]:[28,421 ]<>[8,134 ]:[18,285 ]<>[18,285 ]. Avg. dist.: 4.444773 (1,11,110,1088,8343,10067) transm.: 87202 adjlist NX

Former result, Order = 19500
Communicated by Eyal Loz, Math Dep., Auckland Univ., New Zealand (July 2006)
Voltage graph Z_60 x(17) Z_325, B(1,5), voltages [(234,30)|(179,5)(178,38)(283,1)(285,10)(306,46)]
Z_m x(a) Z_n represents a semidirect product of cyclic groups [x,y][u,v]= [x + u mod m, y*a^u + v mod n].
::: Link to Eyal Loz's original data.
E. Loz, J. Širáň. New record graphs in the degree-diameter problem. Australas. J. Combin. 41 (2008), 63–80.
Com_29621
Degree= 12, Diameter =5; Order = 29621; Moore bound = 193260.
Cayley graph. Found as a semidirect product, 29621 nodes and 177726 edges (F.Comellas 2024):
  1. Z_19 x(392) Z_1559, generators [7,150 ]<>[12,1102 ]:[11,904 ]<>[8,656 ]:[4,1484 ]<>[15,179 ]:[13,654 ]<>[6,1525 ]:[16,759 ]<>[3,538 ]:[15,338 ]<>[4,1069 ]. Avg. dist.: 4.479136 (1,12,132,1442,12100,15934) transm.: 132672. adjlist NX
  2. Z_19 x(781) Z_1559, generators [2,1182]<>[17,514]:[3,458]<>[16,153]:[1,1411]<>[18,1138]:[8,1363]<>[11,447]:[3,180]<>[16,986]:[5,968]<>[14,559 ]. Avg. dist.:4.475895 (1,12,132,1434,12212,15830) transm.: 132576. adjlist NX
  3. Z_19 x(1205) Z_1559, generators [4,358 ]<>[15,94 ]:[15,963 ]<>[4,1213 ]:[12,47 ]<>[7,639 ]:[9,233 ]<>[10,188 ]:[14,645 ]<>[5,955 ]:[12,1195 ]<>[7,1453]. Avg. dist.: 4.471033 (1,12,132,1452,12320,15704) transm.: 132432. adjlist NX
  4. Z_19 x(1040) Z_1559, generators [18,1182 ]<>[1,771 ]:[4,281 ]<>[15,39 ]:[18,1315 ]<>[1,1202 ]:[8,94 ]<>[11,39 ]:[5,1458 ]<>[14,1108 ]:[17,1436 ]<>[2,1094 ]. Avg. dist.: 4.482647 (1,12,132,1422,12036,16018) transm.: 132776. adjlist NX

Former result, Order = 29470
Communicated by Eyal Loz, Math Dep., Auckland Univ., New Zealand (July 2006)
Voltage graph Z_70 x(27) Z_421, B(0,6), voltages [(57,207)(49,411)(61,245)(18,280)(38,87)(36,238)], avg. dist.: 4.477078 (1,12,132,1434,12098,15793) transm.: 131935
Z_m x(a) Z_n represents a semidirect product of cyclic groups [x,y][u,v]= [x + u mod m, y*a^u + v mod n].
::: Link to Eyal Loz's original data. --- adjlist NX version.
E. Loz, J. Širáň. New record graphs in the degree-diameter problem. Australas. J. Combin. 41 (2008), 63–80.
Found also as a semidirect product, with a lower average distance (F.Comellas 2024):
Z_70 x(27) Z_421 with generators [23,319]<>[47,226]:[21,183]<>[49,53]:[15,305]<>[55,24]:[30,108]<>[40,99]:[22,317]<>[48,80]:[36,176]<>[34,165]. Avg.dist.: 4.472123 (1,12,132,1440,12232,15653) transm.: 131789 adjlist NX
Com_40488
Degree= 13, Diameter =5; Order = 40488; Moore bound = 294073.
Cayley graph. Found as a semidirect product, 40488 nodes and 263172 edges (F.Comellas 2024):
  1. Z_24 x(362) Z_1687 generators [1,1454]<>[23,1189]:[5,1427]<>[19,1090]:[2,1659]<>[22,112]:[15,837]<>[9,1635]:[13,1606]<>[11,320]:[19,1105]<>[5,696]:[12,1029]<>[12,1029]. Avg. dist.:4.479784 (1,13,156,1836,16870,21612) transm.: 181373 adjlist NX
  2. Z_24 x(514) Z_1687 generators [15,1240]<>[9,568]:[13,779]<>[11,1026]:[21,1361]<>[3,766]:[15,1470]<>[9,238]:[1,218]<>[23,912]:[6,765]<>[18,278]:[12,1484]<>[12,1484]. Avg. dist.: 4.481636 (1,13,156,1829,16809,21680) transm.: 181448 adjlist NX

Former result, Order = 40260
Communicated by Eyal Loz, Math Dep., Auckland Univ., New Zealand (July 2006)
Voltage graph Z_60 x(82) Z_671, B(1,6), voltages [(30,0)|(45,205)(50,482)(7,160)(17,585)(39,405)(39,419)]
Z_m x(a) Z_n represents a semidirect product of cyclic groups [x,y][u,v]= [x + u mod m, y*a^u + v mod n].
::: Link to Eyal Loz's original data.
E. Loz, J. Širáň. New record graphs in the degree-diameter problem. Australas. J. Combin. 41 (2008), 63–80.
Com_58095
Degree= 14, Diameter =5; Order = 58095; Moore bound = 433174.
Cayley graph. Found as a semidirect product, 58095 nodes and 406665 edges (F.Comellas 2024):
  1. Z_45 x(191) Z_1291 generators [31,28 ]<>[14,108 ]:[32,290 ]<>[13,507 ]:[28,326 ]<>[17,1177 ]:[41,665 ]<>[4,735 ]:[18,278 ]<>[27,397 ]:[24,148 ]<>[21,1269 ]:[36,259 ]<>[9,957 ]. Avg. dist.: 4.503047 (1,14,182,2362,23544,31992) transm.: 261600 adjlist NX
  2. Z_45 x(365) Z_1291 generators [36,999 ]<>[9,497 ]:[37,431 ]<>[8,865 ]:[3,144 ]<>[42,813 ]:[17,543 ]<>[28,1212 ]:[25,623 ]<>[20,39 ]:[26,454 ]<>[19,1087 ]:[33,437 ]<>[12,719 ]. Avg. dist.:4.507316 (1,14,182,2346,23328,32224) transm.: 261848 adjlist NX

Former result, Order = 57837
Communicated by Eyal Loz, Math Dep., Auckland Univ., New Zealand (July 2006)
Voltage graph Z_39 x(28) Z_1483, B(0,7), voltages [(1,339)(37,997)(32,867)(6,214)(32,581)(21,316)(31,606)]
Z_m x(a) Z_n represents a semidirect product of cyclic groups [x,y][u,v]= [x + u mod m, y*a^u + v mod n].
::: Link to Eyal Loz's original data.
E. Loz, J. Širáň. New record graphs in the degree-diameter problem. Australas. J. Combin. 41 (2008), 63–80.
Com_77520
Degree= 15, Diameter = 5; Order =77520; Moore bound=620565
Cayley graph. Found as a semidirect product, 77520 nodes and 581400 edges (F.Comellas 2024):
  1. Z_48 x(277) Z_1615 generators [42,655]<>[6,390]:[5,1023]<>[43,1021]:[38,1358]<>[10,528]:[39,710]<>[9,1000]:[30,1428]<>[18,833]:[4,757]<>[44,933]:[1,162]<>[47,804]:[24,380]<>[24,380]
    Degree Distribution: [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,77520] Avg. dist.: 4.523833 (1,15,210,2878,30466,43950) transm.: 350683 adjlist NX
  2. Z_48 x(772) Z_1615 generators [3,482]<>[45,406]:[28,1131]<>[20,1239]:[31,682]<>[17,1346]:[47,1424]<>[1,487]:[2,831]<>[46,16]:[10,300]<>[38,785]:[23,1068]<>[25,1339]:[24,0]<>[24,0]
    Degree Distribution: [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,77520] Avg. dist.:4.517228 (1,15,210,2877,30980,43437) transm.: 350171 adjlist NX

Former result, Order = 76860
Cayley graph. Found as a semidirect product, 76860 nodes and 576450 edges (F.Comellas 2024):

Former result, Order = 76518
Communicated by Eyal Loz, Math Dep., Auckland Univ., New Zealand (July 2006)
Voltage graph Z_33 x(79) Z_2317, B(0,3), voltages [(40,5722)(12,5970)(44,3528)]
Z_m x(a) Z_n represents a semidirect product of cyclic groups [x,y][u,v]= [x + u mod m, y*a^u + v mod n].
::: Link to Eyal Loz's original data.
E. Loz, J. Širáň. New record graphs in the degree-diameter problem. Australas. J. Combin. 41 (2008), 63–80.
(⊗ H3)′
Delta= 16, Diam= 5; N=132496; Moore bound= 867857;
The component with polarity of the cartesian product of the incidence graph of regular generalized hexagon H_3 by itself
C. Delorme. Large bipartite graphs with given degree and diameter. J. Graph Theory, 9 (1985) 325–334. link to the paper