Geometry and Dynamics of Singular Symplectic Manifolds

IHP, Paris, November-December 2017, Salle 314

This course is done in the framework of Eva Miranda's Chaire d'Excellence de la Fondation Sciences Mathématiques de Paris

Poster/affiche

Official webpage: https://www.sciencesmaths-paris.fr/fr/le-cours-deva-miranda-933.htm

Annonce: Exceptionnellement, mardi 12 Décembre le cours aura lieu à la Salle 201 de l'IHP

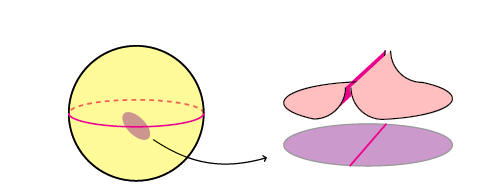
Summary: b-Calculus was introduced by Richard Melrose when considering pseudodifferential operators on manifolds with boundary. Later on, Ryszard Nest and Boris Tsygan applied these ideas to study the deformation quantization of symplectic manifolds with boundary.

The purpose of this minicourse is to unravel the geometrical structures (b-symplectic structures) behind this picture and describe some applications to Dynamical systems. b-Symplectic manifolds are Poisson manifolds which are symplectic away from an hypersurface and satisfy some transversality condition. b-Symplectic manifolds lie "close enough" to the symplectic category and indeed their study can be addressed using an "extended" De Rham complex. In particular many peculiarities from Symplectic manifolds are shared with b-symplectic manifolds. Using these ideas, we will study normal form theorems, action-angle theorems, toric actions and applications to KAM theory. At the end of the minicourse we present other singular symplectic structures such as folded symplectic structures and b^m-symplectic structures (for which the transversality condition is relaxed) and explain how they are related to b-symplectic and symplectic structures.

We will give a general overview of the theory using some examples in celestial mechanics as leitmotiv. For some of them (like double collision), we can even construct b^m-symplectic structures and m-folded structures. This apparent "duality" will be used as an excuse to closely explore the relation between the $b^m$-symplectic category with the symplectic and folded symplectic category. This relation depends surprisingly on the parity of m and is given by a desingularization procedure called deblogging. Time permitting, several applications of deblogging to dynamics and quantization will be presented.

Syllabus/Scheme of the lectures

1. Lecture 1: Introduction. Poisson manifolds: First Examples.

2. Lecture 2: Classical examples. The language of bivector fields. Multivector calculus and the Schouten bracket. Symplectic foliations.

3. Lecture 3:  Weinstein's splitting theorem and normal forms. Conn's linearization theorem. Poisson Cohomology computation kit.

4. Lecture 4: Poisson cohomology and integrable systems on Poisson manifolds.

5. Lecture 5:  Part I: Proof of existence of action-angle coordinates in Poisson Geometry. Part II: Introduction to b-Poisson Geometry.

6. Lecture 6:  Part I: Examples in b-Poisson Geometry. b-Darboux theorem. Modular vector fields in Poisson Geometry. Part II: Codimension one symplectic foliations and unimodular Poisson structures.

7. Lecture 7:  Part I Poisson Geometry of the critical hypersurface of a b-Poisson manifold. Part II. Changing the glasses: A dual language for b-Poisson manifolds.

8. Lecture 8:  Part I: Correction of assignments Part II. b-Symplectic structures. The b-complex. Mazzeo-Melrose formula. b-Cohomology and Poisson Cohomology.

9. Lecture 9: (Salle 201-IHP) Part I: The path method in b-Symplectic Geometry: Relative and global. Applications to classification theorems in b-symplectic geometry (including Radkos' theorem, Delzant theorem and action-angle coordinates for $b$-symplectic manifolds) PartII: Other singular symplectic forms. Introduction to Deblogging: The magic stick. How to convert a $b^m$-symplectic manifold into a (folded) symplectic one.

10. Lecture 10: Applications of Deblogging to Geometry and Topology of b-manifolds, to Dynamics and Quantization. Open problems (and open problems for the Working group).

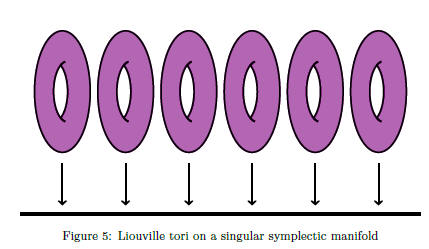
Material:

• Introduction to the course in pdf (slides of November 14)
• A multivectorfield calculus survival kit.
• nov162017.pdf
• Slides of November 21 and November 23
• A list of problems in Poisson Geometry. Some solutions.
• List of open problems.
• Some slides for December 12 and 14: lesson9.pdf, lesson10.pdf

Videos of the course:

Available in the webpage of the course at FSMP:https://www.sciencesmaths-paris.fr/fr/le-cours-deva-miranda-933.htm

Bibliography:

• [BDMOP] R. Braddell, A. Delshams, E. Miranda, C. Oms and A. Planas, An invitation to Singular Symplectic Geometry , arXiv:1705.03846, accepted at International Journal of Geometric Methods in Modern Physics, 2017.
• [CGP] A. Cannas, V. Guillemin, A.R. Pires, Symplectic Origami , International Mathematics Research Notices, no.18, pp 4252-4293, 2011.
• [DKM] A. Delshams, A. Kiesenhofer, E. Miranda, Examples of integrable and non-integrable systems on singular symplectic manifolds, J. Geom. Phys. 115 (2017), 89–97.
• [DZ] Dufour, Jean-Paul; Zung, Nguyen Tien Poisson structures and their normal forms. Progress in Mathematics, 242. Birkhäuser Verlag, Basel, 2005. xvi+321 pp. ISBN: 978-3-7643-7334-4; 3-7643-7334-2
• [DKRS] A. Delshams, V. Kaloshin, A de la Rosa, T. M.-Seara, Global instability in the elliptic restricted three body problem, arXiv:1501.01214.
• [Du] J.J. Duistermaat, On global action-angle coordinates. Comm. Pure Appl. Math. 33 (1980), no. 6, 687-706.
• [GMP1] V. Guillemin, E. Miranda, and A. Pires, Codimension one symplectic foliations and regular Poisson structures. Bull. Braz. Math. Soc. (N.S.), 42(4):607-623, 2011.
• [GMP2] V. Guillemin, E. Miranda, and A. Pires, Symplectic and Poisson geometry on b-manifolds. Adv. Math. 264 (2014), 864-896.
• [GMPS1] V. Guillemin, E. Miranda, A. R. Pires and G. Scott, Toric actions on b-symplectic manifolds, Int Math Res Notices Int Math Res Notices (2015) 2015 (14): 5818-5848.
• [GMPS2] V. Guillemin, E. Miranda, A. Pires, and G. Scott. Convexity for Hamiltonian torus actions on b-symplectic manifolds, Math. Res. Lett. 24 (2017), no. 2, 363–377.
• [GMW1] V. Guillemin, E. Miranda, J. Weitsman, Desingularizing b^m-symplectic structures,
  International Mathematics Research Notices, rnx126, https://doi.org/10.1093/imrn/rnx126
• [GMW2] V. Guillemin, E. Miranda, J. Weitsman, On geometric quantization of b-symplectic manifolds ,arXiv:1608.08667.
• [LMV] C. Laurent-Gengoux, E. Miranda and P. Vanhaecke, Action-angle coordinates for integrable systems on Poisson manifolds. Int. Math. Res. Not. IMRN 2011, no. 8, 1839–1869.
• [LPV] Laurent-Gengoux, Camille; Pichereau, Anne; Vanhaecke, Pol Poisson structures. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], 347. Springer, Heidelberg, 2013. xxiv+461 pp. ISBN: 978-3-642-31089-8.
• [MG]R. McGehee, Singularities in classical celestial mechanics. Proceedings of the International Congress of Mathematicians (Helsinki, 1978), pp. 827-834, Acad. Sci. Fennica, Helsinki, 1980.
• [W] A. Weinstein, The local structure of Poisson manifolds., J. Differential Geom. 18 (1983), no. 3, 523-557.
   

Complementary material:

• Albert Einstein, Zum Quantensatz von Sommerfeld und Epstein, Deutsche Physikalische Gesellschaft, Verhandlungen 19, 82-92 (1917), translation in Portuguese published at Revista Brasileira de Ensino de Fisica, v. 27, n. 1, p. 103 - 107, (2005).
• Kosmann-Schwarzbach, Yvette Les crochets de Poisson, de la mécanique céleste à la mécanique quantique, Siméon-Denis Poisson, 369–401, Hist. Math. Sci. Phys., Ed. Éc. Polytech., Palaiseau, 2013.
• Kosmann-Schwarzbach, Yvette La géométrie de Poisson, création du XXe siècle. (French) [Poisson geometry, a twentieth-century creation] Siméon-Denis Poisson, 129–172, Hist. Math. Sci. Phys., Ed. Éc. Polytech., Palaiseau, 2013.
• Link to the Catalogue  of the Exhibition  "Siméon-Denis Poisson Mathematics at the service of Science" which took place in Paris and Urbana-Champaign in 2014 courtesy of Yvette Kosmann-Schwarzbach, Version en Français ici Catalogue merci à Yvette Kosmann-Schwarzbach.

Related activities of the Chair:

• Working group on b-symplectic geometry and Celestial Mechanics (every Thursday during the course from 4 to 5pm at Salle 314 at Institut Henri Poincaré we discuss about applications of b-Symplectic Geometry to Celestial Mechanics). We are: Roisin Braddell, Eva Miranda, Cédric Oms, Michael Orieux, Wang Qun and anybody who wants to join. Join us!
• Closing conference of the Chair.
• Working group on the n-body problem (on Mondays at Observatoire de Paris)
• Séminaire de Géométrie Hamiltonienne (on Fridays at Jussieu).